One of the most important questions in theoretical physics is finding a theory of quantum gravity, which could help us address fundamental questions about our world, related to what is inside a black hole, or what is the origin of the universe. Several approaches have been developed over the past decades to tackle this problem, with string theory being a leading candidate due to its potential to unify the laws of physics. The mathematical structure of this theory is extremely rich but also incredibly complicated, which makes extracting information about our universe challenging.
In the nineties, G. 't Hooft and L. Susskind introduced the intriguing "holographic principle." This idea suggests that gravity in a given spacetime region can be encoded on a lower-dimensional boundary of that region, similar to how a hologram reconstructs a 3D image from 2D data. This principle allows us to study quantum gravity by examining the boundary of the region of interest. In his seminal work in 1998, J. Maldacena provided an explicit realisation of this principle within string theory, showing that gravity in anti-de Sitter (AdS) spacetime (i.e. spacetime with a negative cosmological constant) can be described by a conformal field theory (CFT) living at the boundary of AdS. CFTs are scale-invariant field theories appearing in many contexts in physics, including phase transitions, and on which we have much mathematical control. This non-trivial correspondence between gravity in the bulk spacetime and field theory (without gravity) at the boundary is a breakthrough that has significantly advanced our understanding of the mathematical structure of fundamental theories.
However, despite the success of the AdS/CFT correspondence, observations have shown that our universe is not AdS; it has a very small positive cosmological constant, prompting the search for a holographic description that aligns more closely with our world. Flat spacetimes (with zero cosmological constant) are especially relevant, as they model astrophysical systems below the cosmological scale and form the basis for many physical theories, including those describing gravitational waves and particle physics. This quest to understand holography in flat space is referred to as "flat space holography."
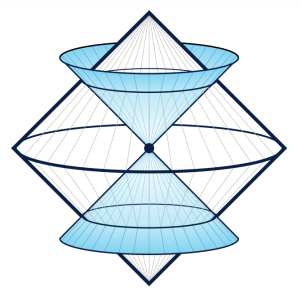
One challenge in flat space holography is the nature of the flat space boundary, defined by the endpoints of light trajectories (null directions). Penrose's conformal compactification reveals that this boundary is null, meaning that any observer living there would move at the speed of light with respect to the interior. The physics of these boundary observers, known as "Carrollian physics," is extremely bizarre. It is characterized by the absence of causality and arbitrary time intervals, reminiscent of what the characters experience in the Mad Tea Party chapter of Lewis Carroll's famous novel Alice in Wonderland. This inspired J.-M. Levy-Leblond in 1965 to coin the name "Carrollian."
My recent work focuses on formulating flat space holography using Carrollian physics at the boundary, known as "Carrollian holography." My goal is to deduce properties of the dual Carrollian theory at the boundary from what we know of gravity in the bulk. The ultimate aim is to find an independent definition for the dual theory, revealing aspects of quantum gravity in the real world. In collaboration with Oxford Mathematicians Luis Fernando Alday, Maria Nocchi and Akshay Yelleshpur Srikant [1], we investigated how Carrollian holography can be derived from the well-established AdS/CFT correspondence by carefully taking the cosmological constant to zero and keeping track of the effects of this limit at the boundary. This work offers valuable insights into extending the holographic principle to flat spacetimes and provides precious hints on how to define the boundary theory intrinsically.
Additionally, I explore connections between Carrollian and celestial holography. This latter approach suggests that gravity in four-dimensional flat spacetime is instead dual to a two-dimensional CFT living on the celestial sphere. Despite the apparent differences between these two approaches, my work demonstrated their equivalence, providing a powerful framework for tackling flat space holography. Key to this understanding is the analysis of correlation functions and the matching of the underlying symmetries, which I am pursuing in collaboration with Oxford Mathematicians Adam Kmec, Lionel Mason and Akshay Yelleshpur Srikant [2,3]. In 2021, A. Strominger discovered a vast algebra of symmetries for scattering amplitudes, known as Lw(1+infinity). These symmetries are thought to be crucial in organising observables in flat spacetime and impose significant constraints on quantum gravity. Part of our work consists of constructing new observables associated with Lw(1+infinity) symmetries, such as conserved quantities, from first principles. This research highlights the fundamental role of Penrose's twistor theory in elucidating these symmetries, positioning Oxford as a beacon in this field of study.
Romain Ruzziconi is a Titchmarsh Research Fellow in Oxford Mathematics.
Image: Illustration of Penrose's conformal compactification. The spacetime boundary is reached by following null directions (in blue).
[1] https://arxiv.org/abs/2406.19343