Statistical mechanics (or thermodynamics) is a way of understanding large systems of interacting objects, such as particles in fluids and gases, chemicals in solution, or people meandering through a crowded street. Large macroscopic systems require prohibitively large systems of equations, and so equilibrium thermodynamics gives us a way to average out all of these details and understand the typical behaviour of the large scale system.
Likely instabilities in stochastic hyperelastic solids
Abstract
Likely instabilities in stochastic hyperelastic solids
L. Angela Mihai
School of Mathematics, Cardiff University, Senghennydd Road, Cardiff, CF24 4AG, UK
E-mail: @email.uk
Nonlinear elasticity has been an active topic of fundamental and applied research for several decades. However, despite numerous developments and considerable attention it has received, there are important issues that remain unresolved, and many aspects still elude us. In particular, the quantification of uncertainties in material parameters and responses resulting from incomplete information remain largely unexplored. Nowadays, it is becoming increasingly apparent that deterministic approaches, which are based on average data values, can greatly underestimate, or overestimate, mechanical properties of many materials. Thus, stochastic representations, accounting for data dispersion, are needed to improve assessment and predictions. In this talk, I will consider stochastic hyperelastic material models described by a strain-energy density where the parameters are characterised by probability distributions. These models, which are constructed through a Bayesian identification procedure, rely on the maximum entropy principle and enable the propagation of uncertainties from input data to output quantities of interest. Similar modelling approaches can be developed for other mechanical systems. To demonstrate the effect of probabilistic model parameters on large strain elastic responses, specific case studies include the classic problem of the Rivlin cube, the radial oscillatory motion of cylindrical and spherical shells, and the cavitation and finite amplitude oscillations of spheres.
Network-based approaches for authorship attribution
Abstract
The problem of authorship attribution (AA) involves matching a text of unknown authorship with its creator, found among a pool of candidate authors. In this work, we examine in detail authorship attribution methods that rely on networks of function words to detect an “authorial fingerprint” of literary works. Previous studies interpreted these word adjacency networks (WANs) as Markov chains, giving transition rates between function words, and they compared them using information-theoretic measures. Here, we apply a variety of network flow-based tools, such as role-based similarity and community detection, to perform a direct comparison of the WANs. These tools reveal an interesting relation between communities of function words and grammatical categories. Moreover, we propose two new criteria for attribution based on the comparison of connectivity patterns and the similarity of network partitions. The results are positive, but importantly, we observe that the attribution context is an important limiting factor that is often overlooked in the field's literature. Furthermore, we give important new directions that deserve further consideration.
Noise in coevolving networks
Abstract
Coupling dynamics of the states of the nodes of a network to the dynamics of the network topology leads to generic absorbing and fragmentation transitions. The coevolving voter model is a typical system that exhibits such transitions at some critical rewiring. We study the robustness of these transitions under two distinct ways of introducing noise. Noise affecting all the nodes destroys the absorbing-fragmentation transition, giving rise in finite-size systems to two regimes: bimodal magnetization and dynamic fragmentation. Noise targeting a fraction of nodes preserves the transitions but introduces shattered fragmentation with its characteristic fraction of isolated nodes and one or two giant components. Both the lack of absorbing state for homogeneous noise and the shift in the absorbing transition to higher rewiring for targeted noise are supported by analytical approximations.
Paper Link:
https://journals.aps.org/pre/abstract/10.1103/PhysRevE.92.032803
14:15
Representations of p-adic groups
Abstract
In the 1990s Moy and Prasad revolutionized the representation theory of p-adic groups by showing how to use Bruhat-Tits theory to assign invariants to representations of p-adic groups. The tools they introduced resulted in rapid advancements in both representation theory and harmonic analysis -- areas of central importance in the Langlands program. A crucial ingredient for many results is an explicit construction of (types for) representations of p-adic groups. In this talk I will indicate why, survey what constructions are known (no knowledge about p-adic groups assumed) and present recent developments based on a refinement of Moy and Prasad's invariants.
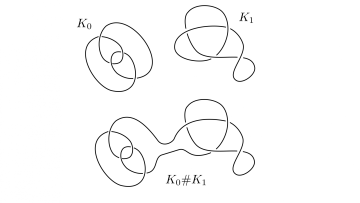
Knots are isotopy classes of smooth embeddings of $S^1$ in to $S^3$. Intuitively a knot can be thought of as an elastic closed curve in space, that can be deformed without tearing. Oxford Mathematician Daniele Celoria explains.
"Knots are ubiquitous in the study of the topological and geometrical properties of manifolds with dimension $3$ and $4$. This is due to the fact that they can be used to prescribe the attachment instructions for the "building blocks" of these spaces, through a process known as surgery.
Talks by Dphil students
Abstract
Tanut Treetanthiploet
---------------------
Exploration vs Exploitation under Statistical Uncertainty
The exploration vs Exploitation trade-off can be quantified and studied through the notion of statistical uncertainty using the theory of nonlinear expectations. The dynamic allocation problem of multi-armed bandits will be discussed. In the case of a finite state space in discrete time, we can describe the value function in terms of the solution to a discrete BSDE and obtain a similar notion to the Bellman equation. We also give an approximation scheme to evaluate decisions in the simple setting.
Julien Vaes
-----------
Optimal Execution Strategy Under Price and Volume Uncertainty
In the seminal paper on optimal execution of portfolio transactions, Almgren and Chriss define the optimal trading strategy to liquidate a fixed volume of a single security under price uncertainty. Yet there exist situations, such as in the power market, in which the volume to be traded can only be estimated and becomes more accurate when approaching a specified delivery time. To meet the need of efficient strategies in these situations, we have developed a model that accounts for volume uncertainty and show that a risk-averse trader has benefit in delaying their trades. We show that the optimal strategy is a trade-off between early and late trades to balance risk associated to both price and volume. With the incorporation of a risk term for the volume to trade, the static optimal strategies obtained with our model avoid the explosion in the algorithmic complexity associated to dynamic programming solutions while yielding to competitive performance.
Strategic Fire-Sales and Price-Mediated Contagion in the Banking System
Abstract
We consider a price-mediated contagion framework in which each bank, after an exogenous shock, may have to sell assets in order to comply with regulatory constraints. Interaction between banks takes place only through price impact. We characterize the equilibrium of the strategic deleveraging problem and we calibrate our model to publicly-available data, the US banks that were part of the 2015 regulatory stress-tests. We then consider a more sophisticated model in which each bank is exposed to two risky assets (marketable and not marketable) and is only able to sell the marketable asset. We calibrate our model using the six banks with significant trading operations and we show that, depending on the price impact, the contagion of failures may be significant. Our results may be used to refine current stress testing frameworks by incorporating potential contagion mechanisms between banks. This is joint work with Yann Braouezec.