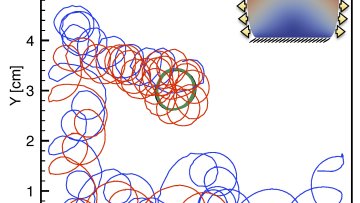
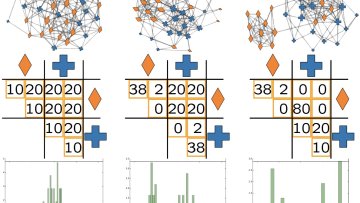
Periodic and localized structures in thin elastic plates
Abstract
Many types of patterns emerging spontaneously can be observed in systems involving thin elastic plates and subjected to external or internal stresses (compression, differential growth, shearing, tearing, etc.). These mechanical systems can sometime be seen as model systems for more complex natural systems and allow to study in detail elementary emerging patterns. One of the simplest among such systems is a bilayer composed of a thin plate resting on a thick deformable substrate. Upon slight compression, periodic undulations (wrinkles) with a well-defined wavelength emerge at the level of the thin layer. We will show that, as the compression increases, this periodic state is unstable and that a second order transition to a localized state (fold) occurs when the substrate is a dense fluid.