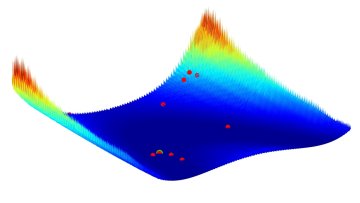
The problem of optimisation – that is, finding the maximum or minimum of an ‘objective’ function – is one of the most important problems in computational mathematics. Optimisation problems are ubiquitous: traders might optimise their portfolio to maximise (expected) revenue, engineers may optimise the design of a product to maximise efficiency, data scientists minimise the prediction error of machine learning models, and scientists may want to estimate parameters using experimental data.
11:00
The Pigeonhole Geometry of Numbers and Sums of Squares
Abstract
Fermat’s two-squares theorem is an elementary theorem in number theory that readily lends itself to a classification of the positive integers representable as the sum of two squares. Given this, a natural question is: what is the minimal number of squares needed to represent any given (positive) integer? One proof of Fermat’s result depends on essentially a buffed pigeonhole principle in the form of Minkowski’s Convex Body Theorem, and this idea can be used in a nearly identical fashion to provide 4 as an upper bound to the aforementioned question (this is Lagrange’s four-square theorem). The question of identifying the integers representable as the sum of three squares turns out to be substantially harder, however leaning on a powerful theorem of Dirichlet and a handful of tricks we can use Minkowski’s CBT to settle this final piece as well (this is Legendre’s three-square theorem).
Divergence-free positive tensors and applications to gas dynamics (2/2)
Abstract
A lot of physical processes are modelled by conservation laws (mass, momentum, energy, charge, ...) Because of natural symmetries, these conservation laws express often that some symmetric tensor is divergence-free, in the space-time variables. We extract from this structure a non-trivial information, whenever the tensor takes positive semi-definite values. The qualitative part is called Compensated Integrability, while the quantitative part is a generalized Gagliardo inequality.
In the first part, we shall present the theoretical analysis. The proofs of various versions involve deep results from the optimal transportation theory. Then we shall deduce new fundamental estimates for gases (Euler system, Boltzmann equation, Vlaov-Poisson equation).
One of the theorems will have been used before, during the Monday seminar (PDE Seminar 4pm Monday 12 November).
All graduate students, post-docs faculty and visitors are welcome to come to the lectures. If you aren't a member of the CDT please email @email to confirm that you will be attending.
Divergence-free positive tensors and applications to gas dynamics (1/2)
Abstract
A lot of physical processes are modelled by conservation laws (mass, momentum, energy, charge, ...) Because of natural symmetries, these conservation laws express often that some symmetric tensor is divergence-free, in the space-time variables. We extract from this structure a non-trivial information, whenever the tensor takes positive semi-definite values. The qualitative part is called Compensated Integrability, while the quantitative part is a generalized Gagliardo inequality.
In the first part, we shall present the theoretical analysis. The proofs of various versions involve deep results from the optimal transportation theory. Then we shall deduce new fundamental estimates for gases (Euler system, Boltzmann equation, Vlaov-Poisson equation).
One of the theorems will have been used before, during the Monday seminar (PDE Seminar 4pm Monday 12 November)
All graduate students, post-docs faculty and visitors are welcome to come to the lectures. If you aren't a member of the CDT please email @email to confirm that you will be attending.
Diophantine approximation is about how well real numbers can be approximated by rationals. Say I give you a real number $\alpha$, and I ask you to approximate it by a rational number $a/q$, where $q$ is not too large. A naive strategy would be to first choose $q$ arbitrarily, and to then choose the nearest integer $a$ to $q \alpha$. This would give $| \alpha - a/q| \le 1/(2q)$, and $\pi \approx 3.14$.
Multiphase flow conditions in metal tapping from Silicon furnaces
Nucleation, Bubble Growth and Coalescence
Abstract
In gas-liquid two-phase pipe flows, flow regime transition is associated with changes in the micro-scale geometry of the flow. In particular, the bubbly-slug transition is associated with the coalescence and break-up of bubbles in a turbulent pipe flow. We consider a sequence of models designed to facilitate an understanding of this process. The simplest such model is a classical coalescence model in one spatial dimension. This is formulated as a stochastic process involving nucleation and subsequent growth of ‘seeds’, which coalesce as they grow. We study the evolution of the bubble size distribution both analytically and numerically. We also present some ideas concerning ways in which the model can be extended to more realistic two- and three-dimensional geometries.
Using signatures to predict amyotrophic lateral sclerosis progression
Abstract
Medical data often comes in multi-modal, streamed data. The challenge is to extract useful information from this data in an environment where gathering data is expensive. In this talk, I show how signatures can be used to predict the progression of the ALS disease.
Detection of Transient Data using the Signature Features
Abstract
In this talk, we consider the supervised learning problem where the explanatory variable is a data stream. We provide an approach based on identifying carefully chosen features of the stream which allows linear regression to be used to characterise the functional relationship between explanatory variables and the conditional distribution of the response; the methods used to develop and justify this approach, such as the signature of a stream and the shuffle product of tensors, are standard tools in the theory of rough paths and provide a unified and non-parametric approach with potential significant dimension reduction. We apply it to the example of detecting transient datasets and demonstrate the superior effectiveness of this method benchmarked with supervised learning methods with raw data.