Thu, 01 Nov 2018
13:00 -
14:00
L4
Ning Wang
(Oxford University)
Thu, 18 Oct 2018
13:00 -
14:00
L4
Dynamic clearing and contagion in an Eisenberg-Noe framework
Zachary Feinstein
(Washington University in St. Louis)
Abstract
We will consider an extension of the Eisenberg-Noe model of financial contagion to allow for time dynamics in both discrete and continuous time. Mathematical results on existence and uniqueness of firm wealths under discrete and continuous-time will be provided. The financial implications of time dynamics will be considered, with focus on how the dynamic clearing solutions differ from those of the static Eisenberg-Noe model.
Oxford Mathematics of Consciousness and Applications Network (OMCAN) is a new network with a focus on bringing mathematics to bear on one of sciences' greatest challenges.
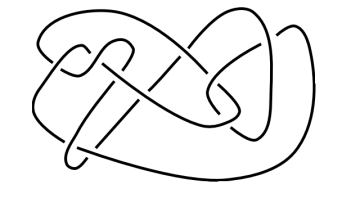
Oxford Mathematician Mehdi Yazdi talks about his study of tangled ropes in 3-dimensional space.
Joint constraints on Galactic diffuse neutrino emission from ANTARES and
IceCube
Albert, A
André, M
Anghinolfi, M
Ardid, M
Aubert, J
Aublin, J
Avgitas, T
Baret, B
Barrios-Martí, J
Basa, S
Belhorma, B
Bertin, V
Biagi, S
Bormuth, R
Boumaaza, J
Bourret, S
Bouwhuis, M
Brânzaş, H
Bruijn, R
Brunner, J
Busto, J
Capone, A
Caramete, L
Carr, J
Celli, S
Chabab, M
Moursli, R
Chiarusi, T
Circella, M
Coelho, J
Coleiro, A
Colomer, M
Coniglione, R
Costantini, H
Coyle, P
Creusot, A
Díaz, A
Deschamps, A
Distefano, C
Palma, I
Domi, A
Donzaud, C
Dornic, D
Drouhin, D
Eberl, T
Bojaddaini, I
Khayati, N
Elsässer, D
Enzenhöfer, A
Ettahiri, A
Fassi, F
Felis, I
Fermani, P
Ferrara, G
Fusco, L
Gay, P
Glotin, H
Grégoire, T
Ruiz, R
Graf, K
Hallmann, S
Haren, H
Heijboer, A
Hello, Y
Hernández-Rey, J
Hößl, J
Hofestädt, J
Illuminati, G
James, C
Jong, M
Jongen, M
Kadler, M
Kalekin, O
Katz, U
Khan-Chowdhury, N
Kouchner, A
Kreter, M
Kreykenbohm, I
Kulikovskiy, V
Lachaud, C
Lahmann, R
Lefèvre, D
Leonora, E
Levi, G
Lotze, M
Loucatos, S
Marcelin, M
Margiotta, A
Marinelli, A
Martínez-Mora, J
Mele, R
Melis, K
Migliozzi, P
Moussa, A
Navas, S
Nezri, E
Nuñez, A
Organokov, M
Păvălaş, G
Pellegrino, C
Piattelli, P
Popa, V
Pradier, T
Quinn, L
Racca, C
Randazzo, N
Riccobene, G
Sánchez-Losa, A
Saldaña, M
Salvadori, I
Samtleben, D
Sanguineti, M
Sapienza, P
Schüssler, F
Spurio, M
Stolarczyk, T
Taiuti, M
Tayalati, Y
Trovato, A
Vallage, B
Elewyck, V
Versari, F
Vivolo, D
Wilms, J
Zaborov, D
Zornoza, J
Zúñiga, J
Aartsen, M
Ackermann, M
Adams, J
Aguilar, J
Ahlers, M
Ahrens, M
Samarai, I
Altmann, D
Andeen, K
Anderson, T
Ansseau, I
Anton, G
Argüelles, C
Auffenberg, J
Axani, S
Backes, P
Bagherpour, H
Bai, X
Barbano, A
Barron, J
Barwick, S
Baum, V
Bay, R
Beatty, J
Tjus, J
Becker, K
BenZvi, S
Berley, D
Bernardini, E
Besson, D
Binder, G
Bindig, D
Blaufuss, E
Blot, S
Bohm, C
Börner, M
Bos, F
Böser, S
Botner, O
Bourbeau, E
Bourbeau, J
Bradascio, F
Braun, J
Brenzke, M
Bretz, H
Bron, S
Brostean-Kaiser, J
Burgman, A
Busse, R
Carver, T
Cheung, E
Chirkin, D
Christov, A
Clark, K
Classen, L
Collin, G
Conrad, J
Coppin, P
Correa, P
Cowen, D
Cross, R
Dave, P
Day, M
André, J
Clercq, C
DeLaunay, J
Dembinski, H
Deoskar, K
Ridder, S
Desiati, P
Vries, K
Wasseige, G
With, M
DeYoung, T
Díaz-Vélez, J
Lorenzo, V
Dujmovic, H
Dumm, J
Dunkman, M
Dvorak, E
Eberhardt, B
Ehrhardt, T
Eichmann, B
Eller, P
Evenson, P
Fahey, S
Fazely, A
Felde, J
Filimonov, K
Finley, C
Franckowiak, A
Friedman, E
Fritz, A
Gaisser, T
Gallagher, J
Ganster, E
Gerhardt, L
Ghorbani, K
Giang, W
Glauch, T
Glüsenkamp, T
Goldschmidt, A
Gonzalez, J
Grant, D
Griffith, Z
Haack, C
Hallgren, A
Halve, L
Halzen, F
Hanson, K
Hebecker, D
Heereman, D
Helbing, K
Hellauer, R
Hickford, S
Hignight, J
Hill, G
Hoffman, K
Hoffmann, R
Hoinka, T
Hokanson-Fasig, B
Hoshina, K
Huang, F
Huber, M
Hultqvist, K
Hünnefeld, M
Hussain, R
In, S
Iovine, N
Ishihara, A
Jacobi, E
Japaridze, G
Jeong, M
Jero, K
Jones, B
Kalaczynski, P
Kang, W
Kappes, A
Kappesser, D
Karg, T
Karle, A
Kauer, M
Keivani, A
Kelley, J
Kheirandish, A
Kim, J
Kintscher, T
Kiryluk, J
Kittler, T
Klein, S
Koirala, R
Kolanoski, H
Köpke, L
Kopper, C
Kopper, S
Koschinsky, J
Koskinen, D
Kowalski, M
Krings, K
Kroll, M
Krückl, G
Kunwar, S
Kurahashi, N
Kyriacou, A
Labare, M
Lanfranchi, J
Larson, M
Lauber, F
Leonard, K
Leuermann, M
Liu, Q
Lohfink, E
Mariscal, C
Lu, L
Lünemann, J
Luszczak, W
Madsen, J
Maggi, G
Mahn, K
Makino, Y
Mancina, S
Maruyama, R
Mase, K
Maunu, R
Meagher, K
Medici, M
Meier, M
Menne, T
Merino, G
Meures, T
Miarecki, S
Micallef, J
Momenté, G
Montaruli, T
Moore, R
Moulai, M
Nagai, R
Nahnhauer, R
Nakarmi, P
Naumann, U
Neer, G
Niederhausen, H
Nowicki, S
Nygren, D
Pollmann, A
Olivas, A
O'Murchadha, A
O'Sullivan, E
Palczewski, T
Pandya, H
Pankova, D
Peiffer, P
Pepper, J
Heros, C
Pieloth, D
Pinat, E
Pizzuto, A
Plum, M
Price, P
Przybylski, G
Raab, C
Rameez, M
Rauch, L
Rawlins, K
Rea, I
Reimann, R
Relethford, B
Resconi, E
Rhode, W
Richman, M
Robertson, S
Rongen, M
Rott, C
Ruhe, T
Ryckbosch, D
Rysewyk, D
Safa, I
Herrera, S
Sandrock, A
Sandroos, J
Santander, M
Sarkar, S
Satalecka, K
Schaufel, M
Schlunder, P
Schmidt, T
Schneider, A
Schöneberg, S
Schumacher, L
Sclafani, S
Seckel, D
Seunarine, S
Soedingrekso, J
Soldin, D
Song, M
Spiczak, G
Spiering, C
Stachurska, J
Stamatikos, M
Stanev, T
Stasik, A
Stein, R
Stettner, J
Steuer, A
Stezelberger, T
Stokstad, R
Stößl, A
Strotjohann, N
Stuttard, T
Sullivan, G
Sutherland, M
Taboada, I
Tenholt, F
Ter-Antonyan, S
Terliuk, A
Tilav, S
Toale, P
Tobin, M
Tönnis, C
Toscano, S
Tosi, D
Tselengidou, M
Tung, C
Turcati, A
Turley, C
Ty, B
Unger, E
Elorrieta, M
Usner, M
Vandenbroucke, J
Driessche, W
Eijk, D
Eijndhoven, N
Vanheule, S
Santen, J
Vraeghe, M
Walck, C
Wallace, A
Wallraff, M
Wandler, F
Wandkowsky, N
Watson, T
Waza, A
Weaver, C
Weiss, M
Wendt, C
Werthebach, J
Westerhoff, S
Whelan, B
Whitehorn, N
Wiebe, K
Wiebusch, C
Wille, L
Williams, D
Wills, L
Wolf, M
Wood, J
Wood, T
Woolsey, E
Woschnagg, K
Wrede, G
Xu, D
Xu, X
Xu, Y
Yanez, J
Yodh, G
Yoshida, S
Yuan, T
Gaggero, D
Grasso, D
Astrophysical Journal Letters
volume 868
L20-L20
(20 Nov 2018)
http://arxiv.org/abs/1808.03531v2
IceCube
A computational approach to hyperspectral imaging for long-range target identification
Vary, S
Thompson, A
Humphreys, D
Tanner, J
Lamb, R
volume 10644
106440q
(08 May 2018)