Oxford Mathematician and Charles Simonyi Professor for the Public Understanding of Science in the University of Oxford, Marcus du Sautoy, has been named one of London's most influential mathematicians in the London Standard Progress 1000 awards. The Progress 1000, in partnership with Citi, is an annual event hosted by The London Evening Standard to celebrate the people whose influence across many spheres of London life is fel
14:30
Finding interesting patterns using submodular function optimization
14:00
14:30
Solving commutators while preserving structure
Abstract
Nested commutators of differential operators appear frequently in the numerical solution of equations of quantum mechanics. These are expensive to compute with and a significant effort is typically made to avoid such commutators. In the case of Magnus-Lanczos methods, which remain the standard approach for solving Schrödinger equations featuring time-varying potentials, however, it is not possible to avoid the nested commutators appearing in the Magnus expansion.
We show that, when working directly with the undiscretised differential operators, these commutators can be simplified and are fairly benign, cost-wise. The caveat is that this direct approach compromises structure -- we end up with differential operators that are no longer skew-Hermitian under discretisation. This leads to loss of unitarity as well as resulting in numerical instability when moderate to large time steps are involved. Instead, we resort to working with symmetrised differential operators whose discretisation naturally results in preservation of structure, conservation of unitarity and stability
14:00
Matrix iteration for a Helmholtz problem based on Faber polynomials
14:30
14:00
Finite element approximation of implicitly constituted incompressible flow models
14:30
Multi-index methods for quadrature
Abstract
Multi-index methods are a generalization of multilevel methods in high dimensional problem and are based on taking mixed first-order differences along all dimensions. With these methods, we can accurately and efficiently compute a quadrature or construct an interpolation where the integrand requires some form of high dimensional discretization. Multi-index methods are related to Sparse Grid methods and the Combination Technique and have been applied to multiple sampling methods, i.e., Monte Carlo, Stochastic Collocation and, more recently, Quasi Monte Carlo.
In this talk, we describe and analyse the Multi-Index Monte Carlo (MIMC) and Multi-Index Stochastic Collocation (MISC) methods for computing statistics of the solution of a PDE with random data. Provided sufficient mixed regularity, MIMC and MISC achieve better complexity than their corresponding multilevel methods. We propose optimization procedures to select the most effective mixed differences to include in these multi-index methods. We also observe that in the optimal case, the convergence rate of MIMC and MISC is only dictated by the convergence of the deterministic solver applied to a one-dimensional spatial problem. We finally show the effectiveness of MIMC and MISC in some computational tests, including PDEs with random coefficients and Stochastic Particle Systems.
17:00
“Knowledge gained by experience”: Olaus Henrici – engineer, geometer, and maker of mathematical models
Abstract
The (Danish-born) German mathematician Olaus Henrici (1840–1918) studied in Karlsruhe, Heidelberg and Berlin before making his career in London, first at University College and then, from 1884, at the newly formed Central Technical College where he established a Laboratory of Mechanics. Although Henrici’s original training was as an engineer, he became known as a promoter of projective geometry and as an advocate for the use of mathematical models. In my talk, I shall discuss the different aspects of Henrici's work and explore connections between them.
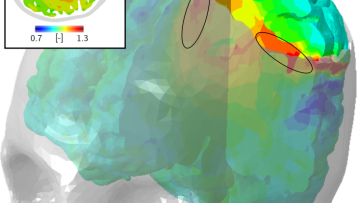
For over a hundred years, when confronted by swelling in the brain, surgeons more often than not have resorted to decompressive craniectomy, the traditional route to reducing swelling by removing a large part of the skull. However, while this might be the standard procedure, its failure rate has been worryingly high, primarily because the consequences on the rest of the brain have been poorly understood.