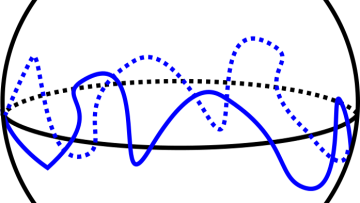
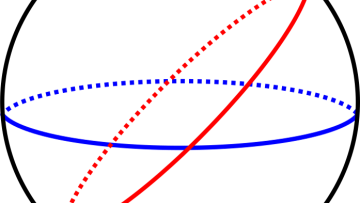
Minimal Lagrangians are key objects in geometry, with many connections ranging from classical problems through to modern theoretical physics, but where and how do we find them? Oxford Mathematician Jason Lotay describes some of his research on these questions.
"A classical problem in geometry going back at least to Ancient Greece is the so-called isoperimetric problem: what is the shortest curve in the plane enclosing a given area A? The answer is a circle:
Stability conditions on triangulated categories were introduced by Bridgeland, based on ideas from string theory. Conjecturally, they control existence of solutions to the deformed Hermitian Yang-Mills equation and the special Lagrangian equation (on the A-side and B-side of mirror symmetry, respectively). I will focus on the symplectic side and sketch a program which replaces special Lagrangians by "spectral networks", certain graphs enhanced with algebraic data. Based on joint work in progress with Katzarkov, Konstevich, Pandit, and Simpson.
In the talk I will discuss the following result and related analytic and geometric questions: On the boundary of any convex body in the Euclidean space there exists at least one infinite geodesic.
