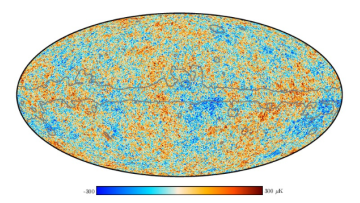
Oxford Mathematicians Dmitry Belyaev and Michael McAuley explain the ubiquitous role of Gaussian Fields in modelling spatial phenomena across science, and especially in cosmology. This case-study is based on work with Stephen Muirhead at Queen Mary University of London (QMUL).
OCIAM learns ... about exponential asymptotics
A new bi-weekly seminar series, 'OCIAM learns...."
Internal speakers give a general introduction to a topic on which they are experts.
Inverting a signature of a path
Abstract
Abstract: The signature of a path is a sequence of iterated coordinate integrals along the path. We aim at reconstructing a path from its signature. In the special case of lattice paths, one can obtain exact recovery based on a simple algebraic observation. For general continuously differentiable curves, we develop an explicit procedure that allows to reconstruct the path via piecewise linear approximations. The errors in the approximation can be quantified in terms of the level of signature used and modulus of continuity of the derivative of the path. The main idea is philosophically close to that for the lattice paths, and this procedure could be viewed as a significant generalisation. A key ingredient is the use of a symmetrisation procedure that separates the behaviour of the path at small and large scales.We will also discuss possible simplifications and improvements that may be potentially significant. Based on joint works with Terry Lyons, and also with Jiawei Chang, Nick Duffield and Hao Ni.
Learning with Signatures: embedding and truncation order selection
Abstract
Abstract: Sequential and temporal data arise in many fields of research, such as quantitative finance, medicine, or computer vision. We will be concerned with a novel approach for sequential learning, called the signature method, and rooted in rough path theory. Its basic principle is to represent multidimensional paths by a graded feature set of their iterated integrals, called the signature. On the one hand, this approach relies critically on an embedding principle, which consists in representing discretely sampled data as paths, i.e., functions from [0,1] to R^d. We investigate the influence of embeddings on prediction accuracy with an in-depth study of three recent and challenging datasets. We show that a specific embedding, called lead-lag, is systematically better, whatever the dataset or algorithm used. On the other hand, in order to combine signatures with machine learning algorithms, it is necessary to truncate these infinite series. Therefore, we define an estimator of the truncation order and prove its convergence in the expected signature model.
14:15
Some constructions of Calabi--Yau threefolds and real Lagrangian submanifolds
Abstract
I will describe the results of two projects on the construction of Calabi-Yau threefolds and certain real Lagrangian submanifolds. The first concerns the construction of a novel dataset of Calabi-Yau threefolds via an application of the Gross-Siebert algorithm to a reducible union of toric varieties obtained by degenerating anti-canonical hypersurfaces in a class of (around 1.5 million) Gorenstein toric Fano fourfolds. Many of these constructions correspond to smoothing such a hypersurface; in contrast to the famous construction of Batyrev-Borisov which exploits crepant resolutions of such hypersurfaces. A central ingredient here is the construction of a certain 'integral affine structure with singularities' on the boundary of a class of polytopes from which one can form a topological model, due to Gross, of the corresponding Calabi-Yau threefold X. In general, such topological models carry a canonical (anti-symplectic) involution i and in the second project, which is joint work with H. Argüz, we describe the fixed point locus of this involution. In particular, we prove that the map i*-1 on graded pieces of a Leray filtration of H^3(X,Z2) can be identified with the map D -> D^2, where D is an element of H^2(X',Z2) and X' is mirror-dual to X. We use this to compute the Z2 cohomology group of the fixed locus, answering a question of Castaño-Bernard--Matessi.
15:30
Bootstrap percolation and kinetically constrained spin models: critical time scales
Part of the Oxford Discrete Maths and Probability Seminar, held via Zoom. Please see the seminar website for details.
Abstract
Recent years have seen a great deal of progress in understanding the behavior of bootstrap percolation models, a particular class of monotone cellular automata. In the two dimensional lattice there is now a quite complete understanding of their evolution starting from a random initial condition, with a universality picture for their critical behavior. Here we will consider their non-monotone stochastic counterpart, namely kinetically constrained models (KCM). In KCM each vertex is resampled (independently) at rate one by tossing a p-coin iff it can be infected in the next step by the bootstrap model. In particular infection can also heal, hence the non-monotonicity. Besides the connection with bootstrap percolation, KCM have an interest in their own : when p shrinks to 0 they display some of the most striking features of the liquid/glass transition, a major and still largely open problem in condensed matter physics.
14:00
Thresholds
Part of the Oxford Discrete Maths and Probability Seminar, held via Zoom. Please see the seminar website for details.
Abstract
I'll discuss our recent proof of a conjecture of Talagrand, a fractional version of the "expectation-threshold" conjecture of Kahn and Kalai. As a consequence of this result, we resolve various (heretofore) difficult problems in probabilistic combinatorics and statistical physics.
14:15
Quantum K-theory and 3d A-model
Abstract
I will discuss some ongoing work on three-dimensional supersymmetric gauge theories and their relationship to (equivariant) quantum K-theory. I will emphasise the interplay between the physical and mathematical motivations and approaches, and attempt to build a dictionary between the two. As an interesting example, I will discuss the quantum K-theory of flag manifolds. The QK ring will be related to the vacuum structure of a gauge theory with Chern-Simons interactions, and the (genus-0) K-theoretic invariants will be computed in terms of explicit residue formulas that can be derived from the relevant supersymmetric path integrals.