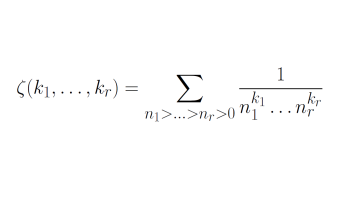Oxford Mathematician Nils Matthes talks about trying to understand old numbers using new techniques.
"The Riemann zeta function is arguably one of the most important objects in arithmetic. It encodes deep information about the whole numbers; for example the celebrated Riemann hypothesis, which gives a precise location of its zeros, predicts deep information about the prime numbers. In my research, I am mostly interested in the special values of the Riemann zeta function at integers k≥2,