Precise forecasting in the first few days of an infectious disease outbreak is challenging. However, Oxford Mathematical Biologist Robin Thompson and colleagues at Cambridge University have used mathematical modelling to show that for accurate epidemic prediction, it is necessary to develop and deploy diagnostic tests that can distinguish between hosts that are healthy and those that are infected but not yet showing symptoms. The data derived from these tests must then be integrated into epidemic models.
16:00
Some smooth applications of non-smooth Ricci curvature lower bounds
Abstract
After a brief introduction to the synthetic notions of Ricci curvature lower bounds in terms of optimal transportation, due to Lott-Sturm-Villani, I will discuss some applications to smooth Riemannian manifolds. These include: rigidity and stability of Levy- Gromov inequality, an almost euclidean isoperimetric inequality motivated by the celebrated Perelman’s Pseudo-Locality Theorem for Ricci flow. Joint work with F. Cavalletti.
The investment decisions made by the construction sector have an obvious impact on the supply of housing. Furthermore, Local Planning Authorities play a fundamental role in shaping this supply via town planning and, in particular, by approving or rejecting planning applications submitted by developers. However, the role of these two factors, as well as their interaction, has so far been largely neglected in models of the housing market.
Over the last five decades, software and computation has grown to become integral to the scientific process, for both theory and experimentation. A recent survey of RCUK-funded research being undertaken in 15 Russell Group universities found that 92% of researchers used research software, 67% reported that it was fundamental to their research, and 56% said they developed their own software.
16:00
A New Northcott Property for Faltings Height
Abstract
The Faltings height is a useful invariant for addressing questions in arithmetic geometry. In his celebrated proof of the Mordell and Shafarevich conjectures, Faltings shows the Faltings height satisfies a certain Northcott property, which allows him to deduce his finiteness statements. In this work we prove a new Northcott property for the Faltings height. Namely we show, assuming the Colmez Conjecture and the Artin Conjecture, that there are finitely many CM abelian varieties of a fixed dimension which have bounded Faltings height. The technique developed uses new tools from integral p-adic Hodge theory to study the variation of Faltings height within an isogeny class of CM abelian varieties. In special cases, we are able to use these techniques to moreover develop new Colmez-type formulas for the Faltings height.
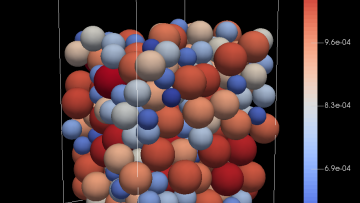
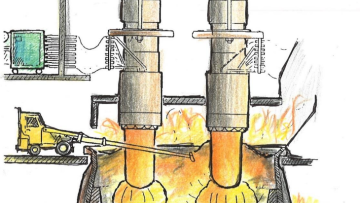
How can solar panels become cheaper? Part of the cost is in the production of silicon, which is manufactured in electrode-heated furnaces through a reaction between carbon and naturally occurring quartz rock. Making these furnaces more efficient could lead to a reduction in the financial cost of silicon and everything made from it, including computer chips, textiles, and solar panels. Greater efficiency also means reduced pollution.
16:00
Antonio Afieri
Abstract
In a recent paper Friedl, Zentner and Livingston asked when a sum of torus knots is concordant to an alternating knot. After a brief analysis of the problem in its full generality, I will describe some effective obstructions based on Floer type theories.
del Pezzo surfaces over imperfect fields
Abstract
We develop a structure theory for del Pezzo surfaces that are regular but geometrically non-normal, based on work of Reid, but now independence on the p-degree of the ground field. This leads to existence results, as well as non-existence results for ground fields of p-degree one. In turn, we settle questions arising from Koll'ar's analysis on the structure of Mori fiber spaces in dimension three. This is joint work with Andrea Fanelli.