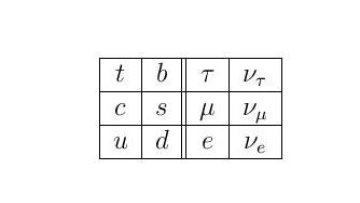
Oxford Mathematician Tsou Sheung Tsun talks about her work on building the Framed Standard Model and the exciting directions it has taken her.
12:00
Characterizations of Besov spaces via ball averages and Bianchini-type norms
Abstract
Motivated by recent problems on mixing flows, it is useful to characterize Besov spaces via oscillation of functions (averages) and minimization problems for bounded variation functions (Bianchini-type norms). In this talk, we discuss various descriptions of Besov spaces in terms of different kinds of averages, as well as Bianchini-type norms. Our method relies on the K-functional of the theory of real interpolation. This is a joint work with S. Tikhonov (Barcelona).
12:00
A non-linear parabolic PDE with a distributional coefficient and its applications to stochastic analysis
Abstract
We consider a non-linear PDE on $\mathbb R^d$ with a distributional coefficient in the non-linear term. The distribution is an element of a Besov space with negative regularity and the non-linearity is of quadratic type in the gradient of the unknown. Under suitable conditions on the parameters we prove local existence and uniqueness of a mild solution to the PDE, and investigate properties like continuity with respect to the initial condition. To conclude we consider an application of the PDE to stochastic analysis, in particular to a class of non-linear backward stochastic differential equations with distributional drivers.