An upper bound for the nonsolvable length of a finite group in terms of its shortest law
Abstract
Every finite group $G$ has a normal series each of whose factors is either a solvable group or a direct product of non-abelian simple groups. The minimum number of nonsolvable factors, attained on all possible such series in G, is called the nonsolvable length $\lambda(G)$ of $G$. In recent years several authors have investigated this invariant and its relation to other relevant parameters. E.g. it has been conjectured by Khukhro and Shumyatsky (as a particular case of a more general conjecture about non-$p$-solvable length) and Larsen that, if $\nu(G)$ is the length of the shortest law holding in the finite group G, the nonsolvable length of G can be bounded above by some function of $\nu(G)$. In a joint work with Francesco Fumagalli and Felix Leinen we have confirmed this conjecture proving that the inequality $\lambda(G) < \nu(G)$ holds in every finite group $G$. This result is obtained as a consequence of a result about permutation representations of finite groups of fixed nonsolvable length. In this talk I will outline the main ideas behind the proof of our result.
Oxford Mathematician Ulrike Tillmann FRS has been appointed Director of the Isaac Newton Institute for Mathematical Sciences and N.M. Rothschild & Sons Professor of Mathematical Sciences at the University of Cambridge.
14:00
Free Energy from Replica Wormholes
Abstract
Recent developments on the black hole information paradox have shown that Euclidean wormholes — so called “replica wormholes’’ — can dominate the von Neumann entropy as computed by a gravitational path integral, and that inclusion of these wormholes results in a unitary Page curve. This development raises some puzzles from the perspective of factorization, and has raised questions regarding what the gravitational path integral is computing. In this talk, I will focus on understanding the relationship between the gravitational path integral and the partition function via the gravitational free energy (more generally the generating functional). A proper computation of the free energy requires a replica trick distinct from the usual one used to compute the entropy. I will show that in JT gravity there is a regime where the free energy computed without replica wormholes is pathological. Interestingly, the inclusion of replica wormholes is not quite sufficient to resolve the pathology: an alternative analytic continuation is required. I will discuss the implications of this for various interpretations of the gravitational path integral (e.g. as computing an ensemble average) and also mention some parallels with spin glasses.
Graduated orders and their lattices
Abstract
For $G$ a finite group, $p$ a prime and $(K, \mathcal{O}_K, k)$ a $p$-modular system the group ring $\mathcal{O}_K G$ is an $\mathcal{O}_k$-order in the $K$-algebra $KG.$ Graduated $\mathcal{O}_K$-orders are a particularly nice class of $\mathcal{O}_K$-orders first introduced by Zassenhaus. In this talk will see that an $\mathcal{O}_K$-order $\Lambda$ in a split $K$-algebra $A$ is graduated if the decomposition numbers for the regular $A$-module are no greater than $1$. Furthermore will see that graduated orders can be described (not uniquely) by a tuple $n$ and a matrix $M$ called the exponant matrix. Finding a suitable $n$ and $M$ for a graduated order $\Lambda$ in the $K$-algebra $A$ provides a parameterisation of the $\Lambda$-lattices inside the regular $A$-module. Understanding the $\mathcal{O}_K G$-lattices inside representations of certain groups $G$ is of interest to those involved in the Langlands programme as well as of independent interest to algebraists.
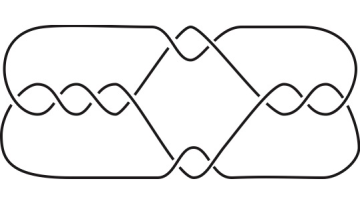
Take a piece of rope and knot it as you wish. When you are done, glue the two extremities together and you will obtain a physical realisation of what mathematicians also call a knot: a simple closed curve in 3-dimensional space. Now, put the knotted rope on a table and take a picture of it from above. It is now a planar projection of your knot. The mathematical equivalent of it is a knot diagram with multiple crossings as shown in the figure.
Totally geodesic submanifolds of symmetric spaces
Abstract
Totally geodesic submanifolds are perhaps one of the easiest types of submanifolds of Riemannian manifolds one can study, since a maximal totally geodesic submanifold is completely determined by any one of its points and the tangent space at that point. It comes as a bit of a surprise then that classification of such submanifolds — up to an ambient isometry — is a nightmarish and widely open question, even on such a manageable and well-understood class of Riemannian manifolds as symmetric spaces.
We will discuss the theory of totally geodesic submanifolds of symmetric spaces and see that any maximal such submanifold is homogeneous and thus can be completely encoded by some Lie algebraic data called a 'Lie triple'. We will then talk about the duality between symmetric spaces of compact and noncompact type and discover that there is a one-to-one correspondence between totally geodesic submanifolds of a symmetric space and its dual. Finally, we will touch on the known classification in rank one symmetric spaces, namely in spheres and projective/hyperbolic spaces over real normed division algebras. Time permitting, I will demonstrate how all this business comes in handy in other geometric problems on symmetric spaces, e. g. in classification of isometric cohomogeneity one actions.
Link: https://teams.microsoft.com/l/meetup-join/19%3ameeting_ZGRiMTM1ZjQtZWNi…
So what really happens every Thursday at 4.30pm UK time?
Is the rumour true that it can both improve your maths AND be a place to hang out with like-minded people and have a bit of a laugh?
We have managed to get hold of this video which reveals all.
Have a watch and join the club
12:45
Confinement in 4d N=1 from 6d N=(2,0)
Abstract
We will discuss confinement in 4d N=1 theories obtained after soft supersymmetry breaking deformations of 4d N=2 Class S theories. Confinement is characterised by a subgroup of the 1-form symmetry group of the theory that is left unbroken in a massive vacuum of the theory. The 1-form symmetry group is encoded in the Gaiotto curve associated to the Class S theory, and its spontaneous breaking in a vacuum is encoded in the N=1 curve (which plays the role of Seiberg-Witten curve for N=1) associated to that vacuum. Using this proposal, we will recover the expected properties of confinement in N=1 SYM theories, and the theories studied by Cachazo, Douglas, Seiberg and Witten. We will also recover the dependence of confinement on the choice of gauge group and discrete theta parameters in these theories.