Oxford Mathematician Robin Thompson has been awarded the Journal of Clinical Medicine “Outstanding Research Award 2020” for his contribution of using mathematical models to represent the epidemiological or evolutionary behavior of infectious disease outbreaks.
Much of the mathematics that is done throughout the world today is essentially European in style. This is a legacy of European colonialism, which saw the export around the globe of a specific approach to mathematics: one derived from the ideas of the ancient Greeks, and based firmly on the notion of proof.
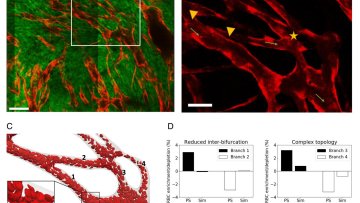
Tissue oxygenation plays a crucial role in the growth of cancerous tumours and their response to treatments. While it may seem intuitive that reducing oxygen delivery to a tumour would be a treatment therapy, low oxygen levels (hypoxia) can significantly reduce the effectiveness of treatments such as radiotherapy and some chemotherapies. Therefore, understanding the dynamics of a tumour's red blood cells - which carry oxygen through the vasculature - is of vital importance.
16:00
Swampland Constraints on 5d N=1 Supergravity
Abstract
We propose Swampland constraints on consistent 5d N=1 supergravity theories. In particular, we focus on a special class of BPS monopole strings which arise only in gravitational theories. The central charges and the levels of current algebras of 2d CFTs on these strings can be computed using the anomaly inflow mechanism and provide constraints for the 5d supergravity using unitarity of the worldsheet CFT. In M-theory, where these theories can be realised by compactification on Calabi-Yau threefolds, the special monopole strings arise from M5 branes wrapping “semi-ample” 4-cycles in the threefolds. We further identify necessary geometric conditions that such cycles need to satisfy and translate them into constraints for the low-energy gravity theory.
Space-time deep neural network approximations for high-dimensional partial differential equations
Abstract
It is one of the most challenging issues in applied mathematics to approximately solve high-dimensional partial differential equations (PDEs) and most of the numerical approximation methods for PDEs in the scientific literature suffer from the so-called curse of dimensionality (CoD) in the sense that the number of computational operations employed in the corresponding approximation scheme to obtain an approximation precision $\varepsilon >0$ grows exponentially in the PDE dimension and/or the reciprocal of $\varepsilon$. Recently, certain deep learning based approximation methods for PDEs have been proposed and various numerical simulations for such methods suggest that deep neural network (DNN) approximations might have the capacity to indeed overcome the CoD in the sense that the number of real parameters used to describe the approximating DNNs grows at most polynomially in both the PDE dimension $d \in \N$ and the reciprocal of the prescribed approximation accuracy $\varepsilon >0$. There are now also a few rigorous mathematical results in the scientific literature which substantiate this conjecture by proving that DNNs overcome the CoD in approximating solutions of PDEs. Each of these results establishes that DNNs overcome the CoD in approximating suitable PDE solutions at a fixed time point $T >0$ and on a compact cube $[a, b]^d$ but none of these results provides an answer to the question whether the entire PDE solution on $[0, T] \times [a, b]^d$ can be approximated by DNNs without the CoD.
In this talk we show that for every $a \in \R$, $ b \in (a, \infty)$ solutions of suitable Kolmogorov PDEs can be approximated by DNNs on the space-time region $[0, T] \times [a, b]^d$ without the CoD.
Linking partition combinatorics to the geometry of Hilbert schemes
Abstract
One of the key objects in studying the Hilbert Scheme of points in the plane is a torus action of $(\mathbb{C}^*)^2$. The fixed points of this action correspond to monomial ideals in $\mathbb{C}[x,y]$, and this gives a connection between the geometry of Hilbert schemes and partition combinatorics. Using this connection, one can extract identities in partition combinatorics from algebro-geometric information and vice versa. I will give some examples of combinatorial identities where as yet the only proofs we have rely on the geometry of Hilbert schemes. If there is time, I will also sketch out a hope that such identities can also be seen by representations of appropriately chosen algebras.
The Springer correspondence for algebraists
Abstract
One of the fundamental examples of geometric representation theory is the Springer correspondence which parameterises the irreducible representations of the Weyl group of a lie algebra in terms of nilpotent orbits of the lie algebra and irreducible representations of the equivariant fundamental group of said nilpotent orbits. If you don’t like geometry this may sound entirely mysterious. In this talk I will hopefully offer a gentle introduction to the subject and present a preprint by Lusztig (2020) which gives an entirely algebraic description of the springer correspondence.