Finite Element Approximation of the Fractional Porous Medium Equation.
CARRILLO, J
FRONZONI, S
SULI, E
Numerische Mathematik
volume abs/2404.18901
Global Convergence of High-Order Regularization Methods with Sums-of-Squares Taylor Models.
Zhu, W
Cartis, C
CoRR
volume abs/2404.03035
(2024)
Strong and Weak Random Walks on Signed Networks
Babul, S
Tian, Y
Lambiotte, R
(12 Jun 2024)
Citizen science for IceCube: Name that Neutrino
Abbasi, R
Ackermann, M
Adams, J
Agarwalla, S
Aguilar, J
Ahlers, M
Alameddine, J
Amin, N
Andeen, K
Anton, G
Argüelles, C
Ashida, Y
Athanasiadou, S
Ausborm, L
Axani, S
Bai, X
Balagopal V., A
Baricevic, M
Barwick, S
Basu, V
Bay, R
Beatty, J
Becker Tjus, J
Beise, J
European Physical Journal Plus
volume 139
issue 6
(18 Jun 2024)
Improved modeling of in-ice particle showers for IceCube event reconstruction
Abbasi, R
Ackermann, M
Adams, J
Agarwalla, S
Aguilar, J
Ahlers, M
Alameddine, J
Amin, N
Andeen, K
Anton, G
Argüelles, C
Ashida, Y
Athanasiadou, S
Ausborm, L
Axani, S
Bai, X
Balagopal V., A
Baricevic, M
Barwick, S
Bash, S
Basu, V
Bay, R
Beatty, J
Becker Tjus, J
Journal of Instrumentation
volume 19
issue 06
(19 Jun 2024)
What Bordism-Theoretic Anomaly Cancellation Can Do for U
Debray, A
Yu, M
Communications in Mathematical Physics
volume 405
issue 7
(19 Jun 2024)
Optimal Control of Collective Electrotaxis in Epithelial Monolayers
Martina-Perez, S
Breinyn, I
Cohen, D
Baker, R
Bulletin of Mathematical Biology
volume 86
issue 8
(19 Jun 2024)
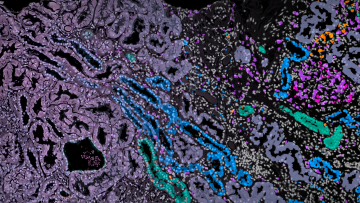
Globally kidney disease is forecast to be the 5th leading cause of death by 2040, and in the UK more than 3 million people are living with the most severe stages of chronic kidney disease. Chronic kidney disease is often due to autoimmune damage to the filtration units of the kidney, known as the glomeruli, which can occur in lupus, a disease which disproportionally affects women and people of non-white ethnicities, groups often underrepresented in research.
Scalable approaches to inference and analysis of genome-wide genealogies
Gunnarsson, Á
Teh, Y
Cohomology Chambers on Complex Surfaces and Elliptically Fibered Calabi–Yau Three-Folds
Brodie, C
Constantin, A
Communications in Mathematical Physics
volume 405
issue 7
(18 Jun 2024)