Graphs

Part of the Oxford MAT Livestream.

Solutions are available here.

MAT syllabus

The graphs of quadratics and cubics. Graphs of
\begin{equation*}
\sin x, \quad \cos x, \quad \tan x, \quad \sqrt{x}, \quad a^x ,\quad \log_a x.
\end{equation*}
Solving equations and inequalities with graphs.

The relations between the graphs
\begin{equation*}
y = f (ax),\quad y = af (x),\quad y = f (x - a), \quad y = f (x) + a
\end{equation*}
and the graph of $y = f (x)$. 

Revision

• The graph of an equation involving $x$ and $y$ is all the points in the $(x,y)$ plane that satisfy the equation. For a function $f(x)$, the graph of $y=f(x)$ shows the value of $f$ at each value of $x$.
• Quadratics $y=ax^2+bx+c$ have graphs like these

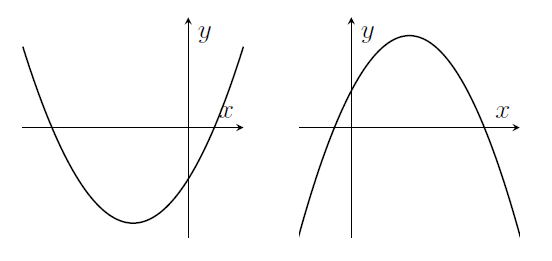
• Cubics \(y=ax^3+bx^2+cx+d\) can have 0 or 1 or 2 turning points.

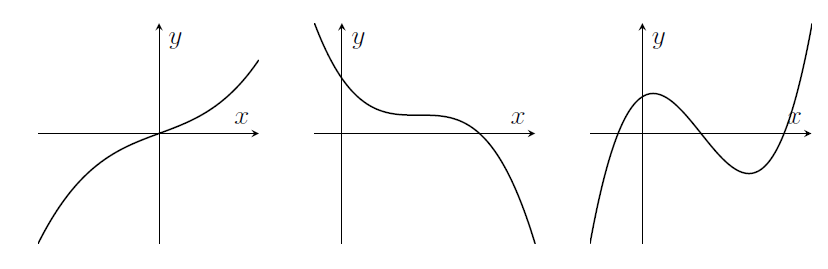
• Other polynomials have graphs that might have more turning points (up to $(n-1)$ turning points if $x^n$ is the highest power of $x$ in the polynomial)
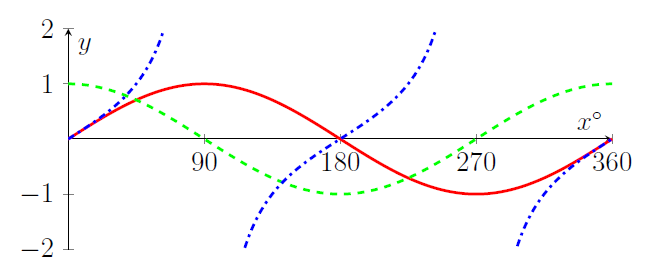
• Graphs of $y=\sin x$ (red solid line) and $y=\cos x$ (green dashed line) and $y=\tan x$ (blue dot-dashed line);

•  Here are some more graphs. Note that $\sqrt{x}=x^{1/2}$ so the derivative is $\frac{1}{2}x^{-1/2}$, which gets arbitrarily large near $x=0$.

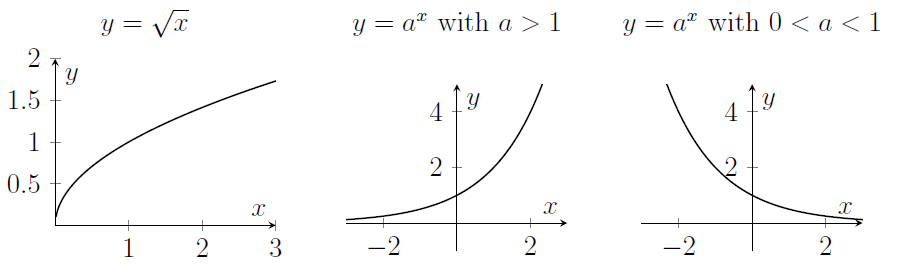
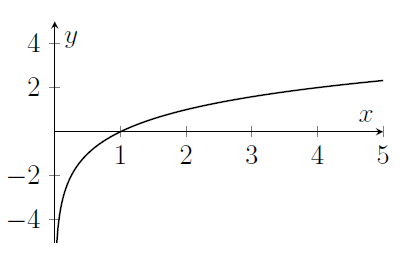
• Here's the graph of $\log_a x$. Note that $\log_a x$ is very negative for $x$ close to zero.

• The graph of $y=f(x-a)$ is the translation of the graph of $y=f(x)$ by a distance $a$ in the positive $x$-direction.
• The graph of $y=f(x)+a$ is the translation of the graph of $y=f(x)$ by a distance $a$ in the positive $y$-direction.
•  The graph of $y=f(ax)$ is a stretch of the graph of $y=f(x)$ by a factor of $\frac{1}{a}$ parallel to the $x$-axis.
• The graph of $y=af(x)$ is a stretch of the graph of $y=f(x)$ by a factor of $a$ parallel to the $y$-axis.

Revision Questions

1. Let $f(x)=x^2+4x+3$. Sketch the graph of $y=f(x+2)$.
   Sketch the graph of $y=3 f( 2 x)$.
   Sketch the graph of $y=2 f( 3 x)$. Is that the same as the previous graph?
   Give an example of a function $g(x)$ such that $y=5g(4x)$ and $y=4g(5x)$ have the same graph.
2. Let $f(x)=x^3-x$. Sketch the graph of $y=2f(x+1)$.
   Sketch the graph of $y=2f(x)+1$. Is that the same as the previous graph?
   Give an example of a function $g(x)$ such that $y=3g(x)+2$ and $y=3g(x+2)$ have the same graph.
3. Sketch the graph of $y=x^n$ for various values of $n$; large, small, negative, positive, zero.
4. Sketch the graph of $\sqrt{4x+1}$ for $x>-\frac{1}{4}$.
5. Sketch the graph of $y=\log_2 x$. Sketch the graph of $y=\log_2 (x^2-2x+1)$.
6. Sketch the graph of $y=\sin(x^2)$.
7. Sketch the graph of $y=\sqrt{x^2}$.
8. Sketch the graphs of $y=2^x$ and $y=\left(\frac{1}{2}\right)^{x}$ on the same axes. Describe the relationship between the graphs.
9. Sketch the graph of $y=\cos 2x$. Sketch the graph of $\displaystyle y=\frac{1}{2} + \frac{1}{2}\cos 2x$.
10. Sketch all the points $(x,y)$ that satisfy $y=4-x$.
    Sketch all the points $(x,y)$ that satisfy $y=4-x^2$.
    Sketch all the points $(x,y)$ that satisfy $y^2=4-x^2$.
11. Let $f(x)=\cos x$. Sketch all the points $(x,y)$ that satisfy $f(x)=f(y)$.
12. Let $f(x)=x^3-x$. Sketch all the points $(x,y)$ that satisfy $f(x)=f(y)$.
13. Sketch all the points $(x,y)$ that satisfy $x^4+2x^2y^2+y^4-3x^2-3y^2+2=0$.
14. Sketch all the points $(x,y)$ that satisfy $x^6+3x^4y^2+3x^2y^4+y^6=1$.
15. Sketch all the points $(x,y)$ that satisfy $xy+x^2y^2=x^3+y^3$.

MAT questions

MAT 2008 Q3

(i) The graph $y=f\left( x\right) $ of a certain function has been plotted below.

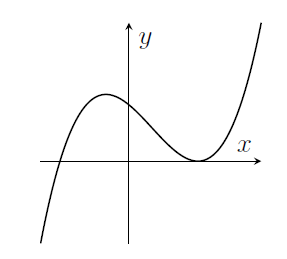
On the next three pairs of axes (A), (B), (C) are graphs of
\begin{equation*}
y=f\left( -x\right) ,\qquad f\left( x-1\right) ,\qquad -f\left( x\right)
\end{equation*}
in some order. Say which axes correspond to which graphs.

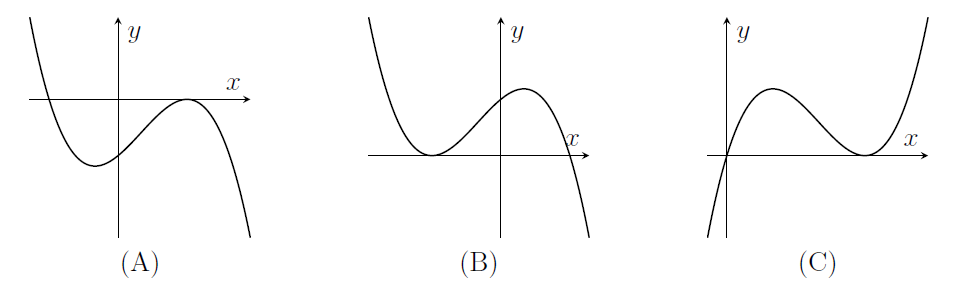
(ii) Sketch, on the same axes, graphs of both of the following functions
\begin{equation*}
y=2^{-x^{2}}\qquad \text{and}\qquad y=2^{2x-x^{2}}.
\end{equation*}
Carefully label any stationary points.

(iii) Let $c$ be a real number and define the following integral
\begin{equation*}
I\left( c\right) =\int_{0}^{1}2^{-\left( x-c\right) ^{2}}\,\text{d}x.
\end{equation*}
State the value(s) of $c$ for which $I\left( c\right) $ is largest. Briefly explain your reasoning.

[Note you are not being asked to calculate this maximum value.]

Hints

(i) Can you identify the graph corresponding to the translation first?

If you really really want to approach this algebraically, try to guess an expression for the function, such as $y=x^3-3x+2$, and then apply the transformations. But it should be possible to think about the transformations without being specific about an expression for the function.

(ii) These two graphs are related by a translation and/or scaling. See if you can find the precise relationship between the two graphs before you sketch either.

For $y=2^{-x^2}$, check what happens for $x$ large, small, positive, negative, zero.

You're not expected to be able to differentiate the functions here. Instead, remember that a stationary point might happen where the function reaches a local maximum. What's the maximum value of each of these functions?

(iii) Remember the extension on the previous worksheet, where we looked at $I(c)$ for a different integral, but where  translation was important. Sketch $2^{-(x-c)^2}$ for various values of $c$.

Extension

[Just for fun, not part of the MAT question]

• The graphs in part (i) have some things in common and some differences.
  List some features of a graph that are unchanged by translations, reflections, or scalings.
  List some features that are may be changed by translations, reflections, or scalings.
• Sketch $y=f(x^2)$ with $f(x)$ as in part (i).
  Sketch $y=f(x)^2$.
  Sketch $y^2=f(x)^2$.
  Sketch $y^2=f(x^2)$.

MAT 2011 Q4

Let $Q$ denote the quarter-disc of points $\left( x,y\right) $ such that $x\geqslant 0,\,y\geqslant 0$ and $x^{2}+y^{2}\leqslant 1$ as drawn in Figures A and B below.

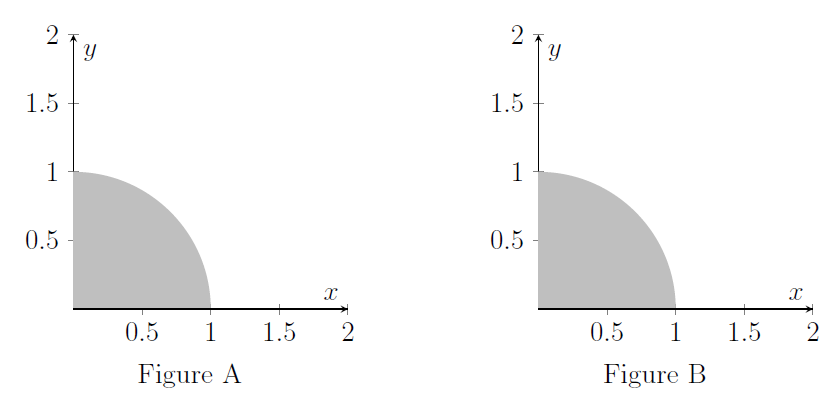
(i) On the axes in Figure A, sketch the graphs of
\begin{equation*}
x+y=\frac{1}{2},\qquad x+y=1,\qquad x+y=\frac{3}{2}.
\end{equation*}

What is the largest value of $x+y$ achieved at points $(x,y)$ in $Q$? Justify your answer.

(ii) On the axes in Figure B, sketch the graphs of 
\begin{equation*}
xy=\frac{1}{4},\qquad xy=1,\qquad xy=2.
\end{equation*}

What is the largest value of $x^{2}+y^{2}+4xy$ achieved at points $\left( x,y\right) $ in $Q$?

What is the largest value of $x^{2}+y^{2}-6xy$ achieved at points $\left( x,y\right) $ in $Q$?

(iii)  Describe the curve
\begin{equation*}
x^{2}+y^{2}-4x-2y=k
\end{equation*}
where $k>-5.$

What is the smallest value of $x^{2}+y^{2}-4x-2y$ achieved at points $\left( x,y\right) $ in $Q$?

Hints

(i) Are there any points that lie in $Q$ and also on the line $x+y=1/2$? If so, we can make $x+y$ at least as large as $1/2$. It helps to draw any $x$-intercepts or $y$-intercepts.

(ii) If $xy=\frac{1}{4}$ then $y=\frac{1}{4}x^{-1}$, so it's not too hard to sketch this function.

How can we make $x^2+y^2$ large? How can we make $xy$ large? Can we do both at the same time?

For $x^2+y^2-6xy$, how can we make $x^2+y^2$ large? How can we make $6xy$ small? Can we do both at the same time?

(iii) I can write that left-hand side as $(x^2-4x+4)+(y^2-2y+1)-5$.

This can be converted to a geometry problem; draw a diagram and mark in any right-angles, known distances, and so on. You should find that when $k$ is as small as possible for some intersection between $x^2+y^2-4x-2y=k$ and $Q$, it is the case that the numbers $2$ and $1$ and $1+\sqrt{k-5}$ are related somehow. Rearrange for $k$.

Extension

[Just for fun, not part of the MAT question]

• Given two circles with centres $C_1$ and $C_2$, describe a process to find, on each circle, the closest point to the other circle.
• Suppose instead that $Q$ is the points $(x,y)$ such that $x\geq 0$ and $y\geq 0$ and $x^4+y^4\leq 1$. Find the largest value of $x^2+y^2+4xy$ achieved at points $(x,y)$ in $Q$.