Graphs Solutions

Part of the Oxford MAT Livestream.

Revision Questions

1. Note that $x^2+4x+3=(x+3)(x+1)$. The graph of $y=f(x+2)$ is the graph of $y=f(x)$ after it has been translated two units to the left.

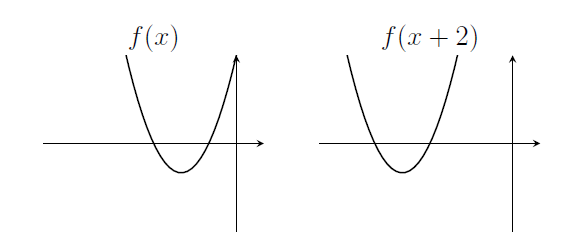
For $y=3f(2x)$, the graph is "squashed" by a factor of 2 parallel to the $x$-axis, then "stretched" by a factor of 3 parallel to the $y$-axis.

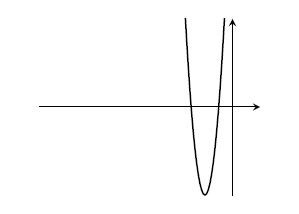
For $y=2 f( 3 x)$, the graph is squashed by a factor of 3 parallel to the $x$-axis, then stretched by a factor of 2 parallel to the $y$-axis

It's not the same as the previous graph. For example, the roots aren't in the same places.

$g(x)=x$ works for the last part; then $y=20x$ in both cases.

2. The graph of $y=f(x)$ and the graph of $y=2f(x+1)$;

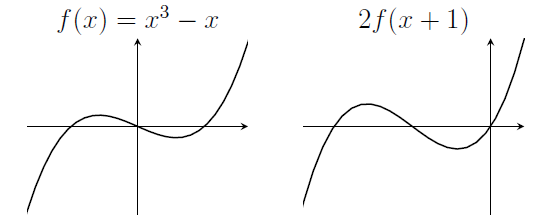
The graph of $y=2f(x)+1$;

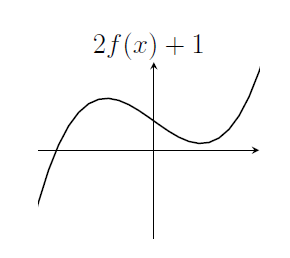
It's not the same as the previous graph. We could compare, for example, the values of $2f(x+1)$ and $2f(x)+1$ when $x=0$.     

$g(x)=x/3+c$ for any constant $c$ works for the last part.

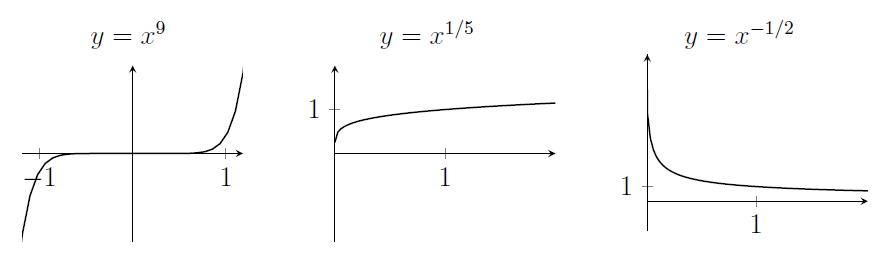
3. For large $n$, $y=x^n$ is close to zero between $-1$ and $1$. For small positive $n<1$, $y=x^n$ is approximately $1$ between $0$ and $1$. For negative $n$, the graph increases to infinity near $x=0$.

4. Note that $\sqrt{4x+1}=2\sqrt{x+\frac{1}{4}}$ so this is a translation of the graph of $y=\sqrt{x}$ by $\frac{1}{4}$ units in the negative $x$-direction followed by a stretch parallel to the $y$-axis with scale factor 2.

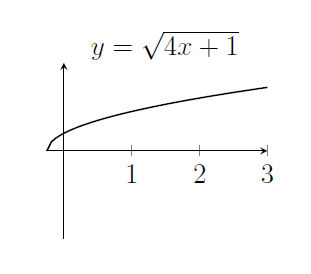
5. Note that $\log_2(x^2-2x+1)=\log_2((x-1)^2)$.

6. The function $\sin(x^2)=0$ when $x^2= 180^\circ n$ for $n$ a whole number, so the graph crosses the $x$-axis more and more frequently as $x$ increases. The graph has reflectional symmetry in the $y$-axis.

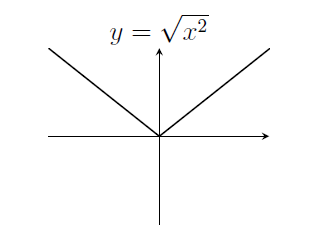
7. If $x\geq0$ then $\sqrt{x^2}=x$ but if $x<0$ then $\sqrt{x^2}=-x$, because $\sqrt{u}$ is always the positive root.

8. The graph of $y=2^x$, and the graph of $y=2^{-x}$.

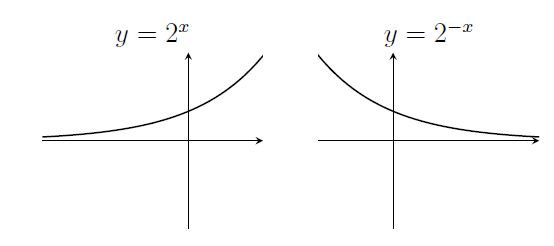
One is the reflection of the other, reflecting in the $y$-axis.

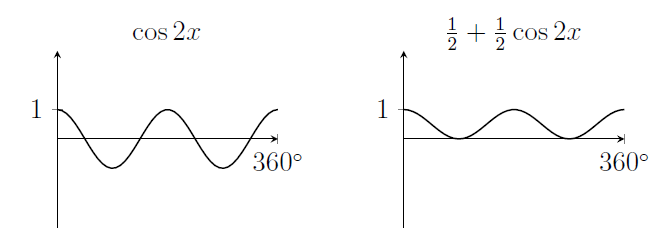
9. The graph of $y=\cos 2x$, and the graph of $y=\frac{1}{2} + \frac{1}{2}\cos 2x$.

10. The equation $y=4-x$ is the equation of a straight line.
The equation $y=4-x^2$ is the equation of a parabola.
The equation $x^2=4-y^2$ is the equation of a circle with radius 2.

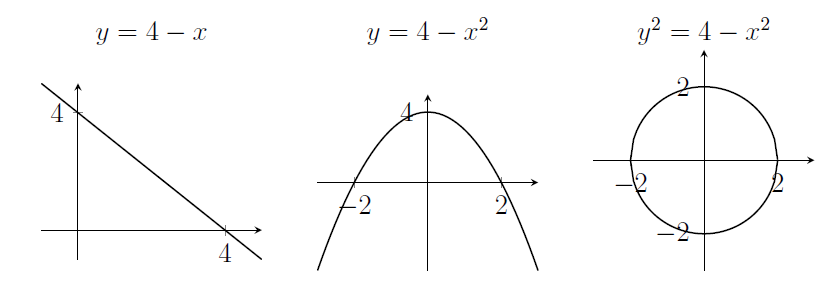
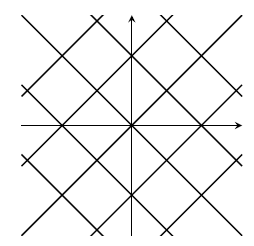
11.. If $\cos x = \cos y$ then either $x=y$, or $x=y+360^\circ n$ for some whole number $n$, or $x+y=360^\circ n$ for some whole number $n$. These are the equations of lines.

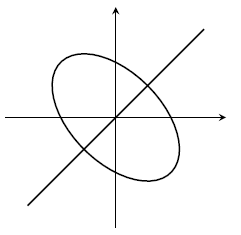
12. It's possible that $x=y$, but because $f(x)=x^3-x$ is not a one-to-one function, there are other points $(x,y)$ that we must consider. For some values of $c$ there are three solutions to $x^3-x=c$.

13. The equation $x^4+2x^2y^2+y^4-3x^2-3y^2+2=0$ simplifies to $(x^2+y^2)^2-3(x^2+y^2)+2=0$, which is a quadratic for $x^2+y^2$, with roots $x^2+y^2=1$ or $x^2+y^2=2$. This is a pair of circles.

14. The equation $x^6+3x^4y^2+3x^2y^4+y^6=1$ simplifies to $(x^2+y^2)^3=1$ so we have $x^2+y^2=1$ and this is a circle.

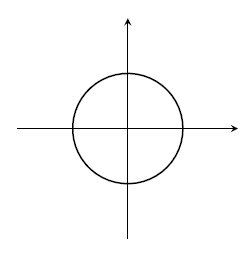
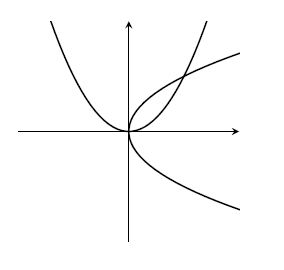
15. The equation rearranges to $x^3-xy=x^2y^2-y^3$. Take out a factor of $x$ on the left and $y^2$ on the right to factorise this as $x(x^2-y)=y^2(x^2-y)$ so either $x^2=y$ or $x=y^2$. This is a pair of parabolas.

MAT Questions

MAT 2014 Q1I

• A translation parallel to the $x$-axis would give us something like $2^{(x-a)^2}$.
• A stretch parallel to the $y$-axis would give us something like $b\times 2^{x^2}$, and if we write $b=2^c$ then this would be $2^{x^2+c}$.
• If we complete the square, we find $x^2-4x+3=(x-2)^2-1$
• So $$2^{x^2-4x+3}=2^{(x-2)^2-1}=2^{(x-2)^2}\times 2^{-1}.$$
• This is what we would get from a translation parallel to the $x$-axis followed by a stretch parallel to the $y$-axis.
• The answer is (b).

MAT 2017 Q1D

• The graph has been reflected in the $x$-axis and reflected in the $y$-axis to get from $y=f(x)$ to $y=-f(-x)$ (you might have used the phrase "stretch by a factor of $-1$", which means the same thing)
• Looking at the graph, there is a point at about $x=1$ where the values of $f(x)$ are very large (either positive or negative), outside the range of this plot. So our transformed graph should have something similar around $x=-1$.
• Looking at the graph again, there are values of $y$ between about $-4$ and $0$ for which there's no graph (there are no values of $x$ such that $y=f(x)$ for those values of $y$). After the reflections, this region will appear between $y=0$ and about $y=4$.
• The overall sort of shape of the graph won't be distorted by the reflections.

• My sketch looks something like this;

  

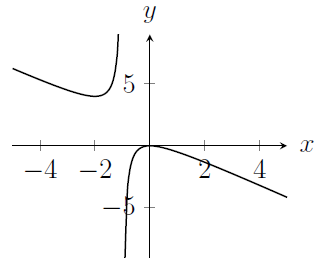
MAT 2008 Q3

(i)  The graph $y=f(-x)$ represents a reflection in the $y$-axis.

The graph $y=f(x-1)$ represents a translation by 1 unit in the positive $x$-direction.

The graph $y=-f(x)$ represents a reflection in the $x$-axis.

Trying these on the graph that we're given for $y=f(x)$, I get something that looks like $(A)$ or $(B)$ for the first and third transformations, while the graph $(C)$ is clearly the translation. Looking at the axes, I can see that $(A)$ is the reflection in the $x$-axis.

So $y=f(-x)$ is $(B)$, $y=f(x-1)$ is $(C)$, and $y=-f(x)$ is $(A)$.

(ii) Note that $-x^2\leq 0$, and gets very negative very quickly as $x$ gets large (no matter whether $x>0$ or $x<0$). We also know that, if $u$ is very negative, then $2^u$ is close to zero. The graph will have reflectional symmetry in the $y$-axis, and the $y$-intercept is $1$.

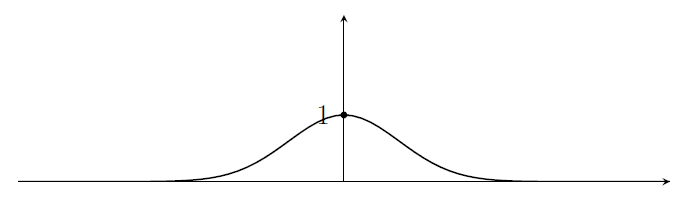
The maximum value of $2^{-x^2}$ comes where $-x^2$ is maximised, which happens when $x=0$. The stationary point here has coordinates $(0,1)$.

Now note that $2x-x^2=-(x-1)^2+1$ if we complete the square. So
$$2^{2x-x^2}=2\times 2^{-(x-1)^2}$$
This is a translation by 1 unit in the positive $x$-direction, followed by a stretch parallel to the $y$-axis with scale factor 2. The $y$-intercept is 1 again, so the graphs intersect there.    After the translations, the stationary point is now at $(1,2)$. My sketch now looks like this;

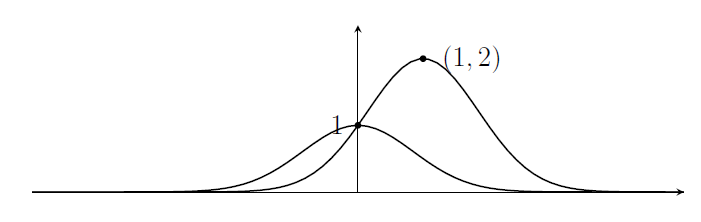
(iii) Note that $2^{-(x-c)^2}$ is just a translation of $2^{-x^2}$. We want the area under the graph between 0 and 1 to be large, so we want the big bit of the graph to be in that range. Let's park it right in the middle with $c=\frac{1}{2}$.

Extension

• Things that are unchanged; number of turning points, degree of the polynomial (if they're polynomials), and more.
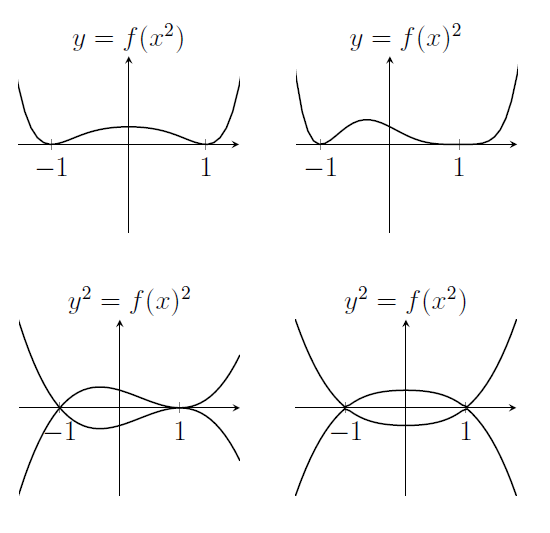
  Things that might change; number of roots, behaviour for large $x$, $y$-intercept, value at $x=37$, and more.
• The graph of $f(x^2)$ just uses the part of the graph of $y=f(x)$ where $x\geq 0$, and there's some distortion. For this function $f(x)$, the values happen to be positive in $x\geq 0$. This graph will have reflectional symmetry in the $y$-axis.
  The graph of $y=f(x)^2$ takes values of $f(x)$ and squares them, so it'll definitely get a positive result. There's no obvious symmetry to this graph.
  If $y^2=f(x)^2$ then either $y=f(x)$ or $y=-f(x)$. This graph will have reflectional symmetry in the $x$-axis.
  For $y^2=f(x^2)$ we have to take our previous graph of $f(x^2)$ and imagine taking the square root of the values, and also the negative of that. This graph will have reflectional symmetry in both the $x$-axis and the $y$-axis.

MAT 2017 Q3

(i) We're being asked to sketch $y=x$ and $y=\sqrt{x}$ and $y=\sqrt[3]{x}$.
 

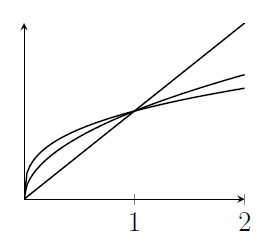
Note that all three graphs pass through the points $(0,0)$ and $(1,1)$.

(ii) The intersection points we found in the previous part are in fact intersection points for any pair of functions $f_k$ and $f_{k+1}$. So the region we're looking at in this part lies between $x=0$ and $x=1$.

To calculate the area between $y=x^{1/k}$ and $y=x^{1/(k+1)}$, we'll need to integrate.
$$\int_0^1 x^{1/(k+1)}-x^{k}\,\mathrm{d}x=\left[\frac{x^{1+1/(k+1)}}{1+1/(k+1)} - \frac{x^{1+1/k}}{1+1/k}\right]_0^1=\frac{k+1}{k+2}-\frac{k}{k+1}.$$

This fraction simplifies a bit, as follows; $$\frac{k+1}{k+2}-\frac{k}{k+1}=\frac{(k+1)^2-k(k+2)}{(k+1)(k+2)}=\frac{1}{(k+1)(k+2)}.$$

The value when $k=1$ is $1/(2\times 3)$.

(ii) First we're looking for the point of intersection of $y=c$ with $y=x$. That's at $(c,c)$.

Then the point of intersection of $y=c$ with $y=\sqrt{x}$ occurs when $x=c^2$, so the point is at $(c^2,c)$.

(iii) The situation is as follows;
 

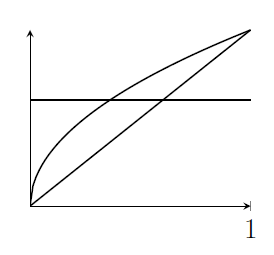
The region above the line $y=c$ looks easier to calculate, to me. I'll find that area by integrating $y=\sqrt{x}$ from $x=c^2$ to $x=1$ and then subtracting a rectangle and a triangle.
 

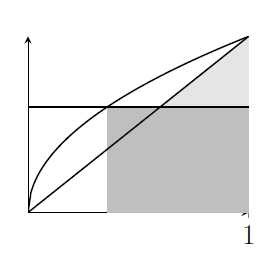
That means that to find the area of the region above the line, I want $$\int_{c^2}^1 \sqrt{x}\,\mathrm{d}x - c(1-c^2)-\frac{1}{2}(1-c)^2$$
which is $$\frac{2}{3}(1-c^3)-c+c^3-\frac{1}{2}+c-\frac{1}{2}c^2.$$
In order for this to be half of the total region between $f_1$ and $f_2$, this area needs to be equal to $\frac{1}{12}$. Simplifying a bit, we want $$\frac{1}{6}+\frac{1}{3}c^3-\frac{1}{2}c^2=\frac{1}{12}$$
Now multiply both sides by 12 and rearrange some more for $4c^3-6c^2+1=0$.

Finally, we're asked to find $c$. It's somewhere between $0$ and $1$. Let's try $1/2$. That works!

There can't be any other solutions in that range, because as the line $y=c$ moves upwards, the area of the region above the line only decreases (so it can't be $\frac{1}{12}$ twice).

Extension

• These areas are easier to calculate if we reflect in the line $y=x$ by switching $y$ and $x$. The curves become $y=x^k$ and $y=x^{k+1}$, and we're looking for the value of $c$ such that the line $x=c$ splits the region between those curves into equal parts. So we just need $$\int_0^c x^{k}-x^{k+1}\,\mathrm{d}x=\frac{1}{2(k+1)(k+2)}$$
  where I've used the result from part (ii).
  This simplifies to the given expression.