Logarithms
Part of the Oxford MAT Livestream.
MAT syllabus
Laws of logarithms and exponentials. Solution of the equation $a^x = b$.
Revision
- $a^ma^n=a^{m+n}$ for any positive real number $a$ and any real numbers $m$ and $n$.
- $(a^m)^n=a^{mn}$ for any positive real number $a$ and any real numbers $m$ and $n$.
- $\displaystyle a^{-n}=\frac{1}{a^n}$ for any positive real number $a$ and any real number $n$.
- \(a^0=1\) for any non-zero real number \(a\).
- The solution to $a^x=b$ where $a$ and $b$ are positive numbers (with $a\neq 1$) is $\log_a (b)$. In this expression, the number $a$ is called the base of the logarithm.
- $\log_a (x)$ is a function of $x$ which is defined when $x>0$. Like with $\sin x$, sometimes the brackets are omitted if it's clear what the function is being applied to, so we might write $\log_a x$.
- $\log_a x$ doesn't repeat any values; if $\log_a x=\log_a y$ then $x=y$.
- Note the special case $\log_a a =1$ because $\log_a a$ is the solution $x$ to the equation $a^x=a$, and that solution is 1.
- In fact, $\log_a (a^x)=x$.
- In that sense, the logarithm function is the inverse function for $y=a^x$.
- It's also true that $a^{\log_a x}=x$. To see why, let $y=\log_a x$. That would mean that $a^y=x$. Now replace the $y$ in that equation with the expression $\log_a x$.
- $\log_a (xy)=\log_a(x)+\log_a(y)$.
- $\log_a (x^k)=k\log_a x$ including $\displaystyle\log_a \frac{1}{x}=-\log_a x$.
- There's a mathematical constant called $e$, which is just a number (it's about 2.7).
- $e^x$ is called the exponential function.
- The laws of indices and laws of logarithms above hold when the base $a$ is equal to $e$.
- $\log_e x$ is sometimes written as $\ln x$ and the function is sometimes called the natural logarithm.
Revision Questions
- Simplify \((2^3)^4\) and \((2^4)^3\) and \(2^42^3\) and \(2^32^4\).
- Solve $x^{-2}+4x^{-1}+3=0$.
- Simplify $\log_{10} 3+\log_{10} 4$ into a single term.
- Write $\log_3(x^2+3x+2)$ as the sum of two terms, each involving a logarithm.
- Solve $\log_x (x^2)=x^3$.
- Solve $\log_x (2x)=3$ for $x>0$.
- Solve $\log_{x+5}(6x+22)=2$.
- Let $a=\ln 2$ and $b=\ln 5$, and write the following in terms of $a$ and $b$.
\begin{equation*}
\ln 1024, \quad \ln 40, \quad \ln \sqrt{\frac{2}{5}}, \quad \ln \frac{1}{10}, \quad \ln 1.024.
\end{equation*} - Expand $\left(e^x+e^{-x}\right)\left(e^y-e^{-y}\right)+\left(e^x-e^{-x}\right)\left(e^y+e^{-y}\right)$.
Expand $\left(e^x+e^{-x}\right)\left(e^y+e^{-y}\right)+\left(e^x-e^{-x}\right)\left(e^y-e^{-y}\right)$. - Solve $2^x=3$. Solve $0.5^x=3$. Solve $4^x=3$.
- For which values of $x$ (if any) does $1^x=1$? For which values of $x$ (if any) does $1^x=3$?
- For what values of \(b\) (if any) does \(0^b=0\)? For what values of \(a\) (if any) does \(a^0=0\)?
- Given $\log_{10}(\log_{10}x)=6$, how many zeros are there at the end of the number $x$?
- Solve $e^{x}+e^{-x}=4$.
How many solutions are there to $e^x+e^{-x}=c$? Identify different cases in terms of $c$. - Prove that $\ln(N+\sqrt{N^2-1})=-\ln(N-\sqrt{N^2-1})$ for any number $N\geq 1$.
- Consider the equation $x^y=y^x$ with $x,y>0$. Use logarithms to turn this into an equation of the form $f(x)=f(y)$.
[Harder] Sketch $f(x)$. - Simplify $a^{k\log_a b}$ for positive numbers $a$, $b$, $k$.
- Consider the number $x=\log_a b \log_b c$. By simplifying $a^x$, show that $x=\log_a c$.
- Similarly, show that $\displaystyle \log_a b = \frac{\log_c b}{\log_c a}$ for positive numbers $a$, $b$, $c$, and hence $\displaystyle \log_a b=\frac{\ln b}{\ln a}$.
MAT questions
MAT 2014 Q1B
The graph of the function $y=\log_{10}\left(x^2-2x+2\right)$ is sketched in
(a)
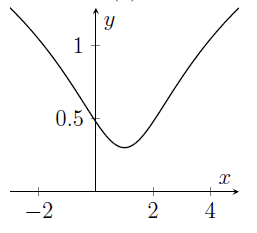
(b)
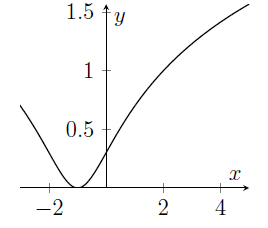
(c)
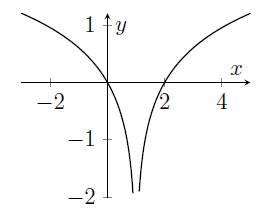
(d)
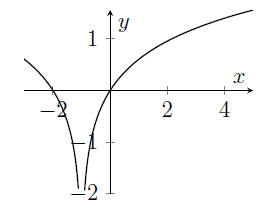
(e)
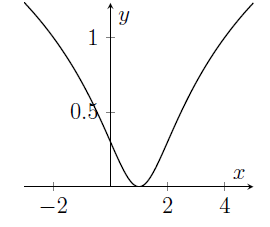
Hints
- It's a good idea to think about the function $x^2-2x+2$ first. Can you say anything about the values which this quadratic takes?
- If you know that $f(x)\geq c$, then you can say that $\log_{10}(f(x))\geq \log_{10} c$. This is because $\log_{10}x$ is an increasing function of $x$ (provided, of course, that $x>0$, where $\log_{10}x$ is defined).
- We could find the coordinates of the minimum of $y=x^2-2x+2$. Then we could infer the coordinates of the minimum of $y=\log_{10}\left(x^2-2x+2\right)$.
MAT 2015 Q1H
How many distinct solutions does the following equation have? $$ \log_{x^2 + 2}(4 - 5x^2 - 6x^3) = 2 $$
(a) None,
(b) 1,
(c) 2,
(d) 3,
(e) Infinitely many.
Hints
- This equation looks horrible, because it combines a polynomial with a logarithm. We could start by factorising the polynomial, or we could start by getting rid of the logarithm.
- Once we've done that, we'll still have the other element of the problem to deal with. We might need to think about separate logarithm terms, or we might need to solve a polynomial.
- If you're solving a polynomial, watch out for repeated roots, because the question asks for distinct solutions.
MAT 2017 Q1I
Let $a,b,c>0$ and $a\neq 1$. The equation $$ \log _b\left(\left(b^x\right)^x\right) + \log_a\left(\frac{c^x}{b^x}\right) + \log_a\left(\frac{1}{b}\right)\log_a(c) = 0 $$
has a repeated root when
(a) $b^2=4ac$,
(b) $\displaystyle b=\frac{1}{a}$,
(c) $\displaystyle c=\frac{b}{a}$,
(d) $\displaystyle c=\frac{1}{b}$,
(e) $a=b=c$.
Hints
- Repeated root reminds me of quadratics and determinants.
- This is a quadratic, if we simplify each term to bring out factors of $x$. You could do that simplification either with laws of logarithms or with power laws.
- Take care; note that the base is different on the first term.
- A quadratic has a repeated root if the discriminant is zero, but it might be easier in this case to just solve the quadratic and write down an equation for the two roots to be equal.
MAT 2008 Q1B
Which is the smallest of these values?
$$ \text{(a)} \quad \log _{10}\pi ,\qquad \text{(b)} \quad \sqrt{\log _{10}\left(\pi ^{2}\right) },\qquad \text{(c)} \quad \left( \frac{1}{\log _{10}\pi }\right)^{3},\qquad \text{(d)} \quad \frac{1}{\log _{10}\sqrt{\pi }} .$$
Hints
- When is $x$ bigger than $\sqrt{2x}$? When is $x$ bigger than $2/x$?
- You'll need to use the fact that $1<\pi<10$, but you shouldn't need to use any more detailed knowledge of the value of $\pi$ than that.
MAT 2008 Q1E
The highest power of $x$ in
\begin{equation*}
\left\{ \left[ \left( 2x^{6}+7\right) ^{3}+\left( 3x^{8}-12\right) ^{4}
\right] ^{5}+\left[ \left( 3x^{5}-12x^{2}\right) ^{5}+\left( x^{7}+6\right)
^{4}\right] ^{6}\right\} ^{3}
\end{equation*}
is
$$ \text{(a)} \quad x^{424},\qquad \text{(b)} \quad x^{450},\qquad \text{(c)} \quad x^{500},\qquad \text{(d)} \quad x^{504}. $$
Hints
- What's the highest power of $x$ in $(2x^6+7)^3$? Do not multiply out! Now look at the other terms too.
- We can ignore the outer-most power of 3 while we're comparing terms, but don't forget about it at the end.
MAT 2010 Q1E
Which is the largest of the following four numbers?
\begin{equation*}
\text{(a)}\quad \log _{2}3,\qquad \text{(b)}\quad \log _{4}8,\qquad \text{(c)
}\quad \log _{3}2,\qquad \text{(d)}\quad \log _{5}10.
\end{equation*}
Hints
- You can evaluate one of these exactly. Which one? Next, I would aim to compare the others to that one.
- Here's a strategy to do that sort of comparison; let's say that we're comparing $\log_2 3$ against $\frac{p}{q}$ for some fraction $\frac{p}{q}$. Is $\log_2 3 < \frac{p}{q}$? Well, if it is, then $3<2^{p/q}$, so $3^q<2^p$. You've got particular values of $p$ and $q$ in mind; go for it!
- You might like to reflect on why it's OK to manipulate the inequalities like this.
MAT 2012 Q1C (modified)
Which is the smallest of the following numbers?
$$\text{(a)} \quad \left(\sqrt{3}\right) ^{3},\qquad \text{(b)} \quad \log _{3}\left( 9^{2}\right),\qquad \text{(c)} \quad \left( 3\sin 60^\circ\right)^{2},\qquad \text{(d)} \quad \log _{2}\left( \log _{2}\left(8^{5}\right) \right).$$
Hints
- Simplify each number as much as you can before doing any comparisons.
Extension
[Just for fun, not part of the MAT question(s)]
- Given a positive number $\alpha$, which is the smallest of these values? Identify the different cases according to $\alpha$.
$$\text{(a)}\quad \alpha,\qquad \text{(b)}\quad \sqrt{2\alpha}, \qquad \text{(c)}\quad \alpha^{-3} \qquad \text{(d)} \quad\frac{2}{\alpha}.$$ - Which is larger, $(8!)^9$ or $(9!)^8$ ?