Logarithms Solutions

Part of the Oxford MAT Livestream.

 

Revision Questions

  1. $(2^3)^4=2^{12}$. $(2^4)^3=2^{12}$. $2^4 2^3=2^7$. $2^3 2^4=2^7$.
  2. This is a quadratic for $\frac{1}{x}$ with solutions $\frac{1}{x}=-1$ or $\frac{1}{x}=-3$. So $x=-1$ or $x=-\frac{1}{3}$. Alternatively, we could multiply both sides by $x^2$ and solve the quadratic that we get.
  3. This is $\log_{10} 12$.
  4. The quadratic inside the brackets factorises, and this is $\log_3(x+2)+\log_3(x+1)$. Other answers are possible, such as $\log_3 (2(x+2))+\log_3((x+1)/2)$.
  5. The left-hand side is just $2$ so we want $2=x^3$. So $x=\sqrt[3]{2}$.
  6. The left-hand side is $1+\log_x 2$ so we want $\log_x 2=2$. So $x^2=2$ and $x=\sqrt{2}$ (not $-\sqrt{2}$ because we're told that $x>0$).
  7. Take $(x+5)$ to the power of each side to get $6x+22=(x+5)^2$. Expand the square and rearrange for $x^2+4x+3=0$. The solutions are $x=-1$ or $x=-3$. Check these solutions; $\log_4(16)=2$ and $\log_2(4)=2$.
  8.  
    • $\ln 1024=\ln\left(2^{10}\right)=10\ln 2=10a$.
    • $\ln 40=\ln 8+\ln 5=3a+b$.
    • $\ln \sqrt{2/5}=\frac{1}{2}\ln 2/5=\frac{1}{2}\left(a-b\right)$.
    • $\ln (1/10)=-\ln 10=-\ln2-\ln 5=-a-b$.
    • $\ln 1.024=\ln 1024+\ln 1/1000=10a +3(-a-b)=7a-3b$.
    • There are other solutions, partly because $b=a\times\log_2 5$.
  9. $e^{x+y}+e^{y-x}-e^{x-y}-e^{-x-y}+e^{x+y}-e^{y-x}+e^{x-y}-e^{-x-y}$. That's $2e^{x+y}-2e^{-x-y}$.
    $e^{x+y}+e^{y-x}+e^{x-y}+e^{-x-y}+e^{x+y}-e^{y-x}-e^{x-y}+e^{-x-y}$. That's $2e^{x+y}+2e^{-x-y}$.
  10. $2^x=3$ is what it means for $x$ to be $\log_2 3$.
    If $0.5^x=3$ then $2^{-x}=3$ so $x=-\log_2 3$. Alternatively, just write down $x=\log_{0.5}3$.
    If $4^x=3$ then $2^{2x}=3$ so $x=\frac{1}{2}\log_2 3$. Alternatively, just write down $x=\log_4 3$.
  11. $1^x=1$ is true for all real $x$. $1^x$ is never equal to 3 for real $x$.
  12. $0^b=0$ for any real $b>0$. $a^0$ is never $0$.
  13. We have $\log_{10}x=10^6$, which is a million. So $x$ is ten to the power of a million. That's got a million zeros at the end.
  14. Multiply both sides by $e^x$ and rearrange to get $e^{2x}-4e^x+1=0$. This is a quadratic for $e^x$. Solve it for $e^x=2\pm \sqrt{3}$. So $x=\ln (2\pm \sqrt{3})$.
    Following the previous working, we can see that we'll get two roots for $e^x$ if $c^2-4>0$. But we need these to be positive roots, so we need $c>2$. If $c=2$ there's a repeated root. If $c<2$ there are no roots.
  15. Move both terms onto the left-hand side and use the fact that $(N+\sqrt{N^2-1})(N-\sqrt{N^2-1})=N^2-(N^2-1)=1$; that's the difference of two squares. Remember that $\ln 1 =0$.
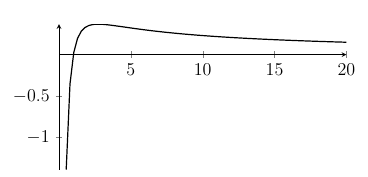
    As a result, our solutions above $x=\ln (2\pm \sqrt{3})$ are actually $x=\pm \ln (2+\sqrt{3})$, revealing a lovely symmetry. But you could have spotted that from the equation, of course!
  16. We have $\ln(x^y)=\ln(y^x)$ which we can simplify down to $y\ln x=x\ln y$. Now rearrange to get $\displaystyle \frac{\ln x}{x}=\frac{\ln y}{y}$. You might choose to put this fraction the other way up, or to square both sides or something, so your $f(x)$ might not be the same as mine. Here's a sketch of $\displaystyle y=\frac{\ln(x)}{x}$.A graph that is very negative near x=0, quickly rises to some positive maximum, then decreases very slowly towards zero.
  17. This is $(a^{\log_a b})^k=b^k$.
  18. We can use a similar bit of algebra to the previous question with $k=\log_b c$.
    $$a^x=a^{\log_a b \log_b c}=\left(a^{\log_a b}\right)^{\log_b c}=\left(b\right)^{\log_b c}=c.$$
    So $a^x=c$ and therefore $x=\log_a c$.
  19. If we relabel the previous result, we can write $\log_c a \log_a b =\log_c b$. Now divide by $\log_c a$ to get
    $$\log_a b = \frac{\log_c b}{\log_c a}$$
    In particular, if we take $c$ to be the number $e$, then we can write that fraction with $\ln$ instead of $\log_e$. This is handy because it shows that we can always write logarithms like $\log_{a} x$ in terms of $\ln$. All other $\log_a x$ graphs are just simple transformations of the $\ln x$ graph.

MAT Questions

MAT 2014 Q1B

  • The function $y=x^2-2x+2=(x-1)^2+1$ if we complete the square.
  • The minimum occurs when $x=1$ and the value at that minimum is $y=1$.
  • Consider now the function $y=\log_{10}(f(x))$ where $f(x)$ is the quadratic above. This graph has a local minimum at $x=1$, and the value there will be $\log_{10}1=0$. Only one of the graphs looks like that.
  • The answer is (e).

MAT 2015 Q1H

  • We can start by using the fact that if $\log_b a = c$ then $a=b^c$.
  • Here $\left(4-5x^2-6x^3\right)=\left(x^2+2\right)^2$.
  • That polynomial simplifies to $x^4+6x^3+9x^2=0$.
  • There's a repeated root at $x=0$, and the polynomial factorises as $x^2(x+3)^2=0$.
  • We should check our solutions; $\log_2(4)=2$ and $\log_{11}(4-5\times 9+6\times27)=\log_{11}(121)=2$.
  • So there are two distinct solutions.
  • The answer is (c).

MAT 2017 Q1I

  • The equation simplifies to $$x^2+x\log_a\left(\frac{c}{b}\right)+\log_a \left(\frac{1}{b}\right)\log_a(c)=0.$$
  • This quadratic factorises as $$\left(x-\log_a\left(b\right)\right)\left(x+\log_a\left(c\right)\right)=0,$$
        where I've used the law of logarithms that $\displaystyle \log_a c -\log_a b =\log_a\left(\frac{c}{b}\right)$.
  • This quadratic has two distinct roots, unless $-\log_a b = \log_a c$. That happens precisely when $\displaystyle c=\frac{1}{b}$.
  • The answer is (d).

MAT 2008 Q1B

Let $x=\log_{10} \pi$. Note that $0<x<1$ because $1<\pi<10$. The four values are
$$
x,\qquad \sqrt{2x}, \qquad x^{-3}\qquad \frac{2}{x}.
$$
Now we want to compare these terms. We have $x<\sqrt{2x}$ if $x^2<2x$ which happens if $x<2$. Also $x<x^{-3}$ because $x<1$. Also $x<2/x$ because $x<\sqrt{2}$.

The answer is (a).

 

MAT 2008 Q1E

Ignore small powers of $x$ inside each pair of round brackets. We get something like
$$
\left\lbrace \left[ \left(2x^6+\dots \right)^3+\left(3x^8+\dots\right)^4\right]^5+\left[ \left( 3x^5+\dots \right)^5 + \left(x^7+\dots\right)^4\right]^6 \right\rbrace ^3
$$
Now apply the powers on the round brackets and compare terms again
$$
\left\lbrace \left[ 2^3x^{18} +3^4x^{32}+\dots\right]^5+\left[ 3^5x^{25}  + x^{28}+\dots\right]^6 \right\rbrace ^3
$$
Take the largest power inside each square bracket and apply the power on that bracket
$$
\left\lbrace 3^{20}x^{160}+ x^{168}+\dots\right\rbrace ^3
$$
Take the largest power inside the curly brackets and apply the power on that bracket
$$
x^{504}+\dots
$$

The answer is (d).

 

MAT 2010 Q1E

First note that $\displaystyle \log_4 8= \frac{3}{2}$ because $4=2^2$ and $8=2^3$, so $4^{3/2}=8$.

Is $\displaystyle\log_2{3}>\frac{3}{2}$? Only if $\displaystyle3>2^{3/2}$ so only if $9>8$. Yes!

Is $\displaystyle\log_3{2}>\frac{3}{2}$? No, it's less than one.

Is $\displaystyle\log_5{10}>\frac{3}{2}$? Only if $10>5^{3/2}$, so only if $100>125$. No!

So only $\log_2 3$ is larger than $\displaystyle\frac{3}{2}$.

The answer is (a).

 

MAT 2012 Q1C

Simplify $(\sqrt{3})^3=3\sqrt{3}$.

Simplify $\log_3(9^2)=4$.

Simplify $\displaystyle (3\sin 60^\circ)^2=(3\sqrt{3}/2)^2=\frac{27}{4}$.

Simplify $\log_2(\log_2 8^5)=\log_2(\log_2 2^{15})=\log_2(15)$.

The next thing I notice is that $15<16$ so $\log_2(15)<4$. Aha, that means that it's less than $\log_3(9^2)$.

Then perhaps I could notice that $\frac{27}{4}>4$. So my remaining candidates for the smallest of the numbers are $3\sqrt{3}$ and $\log_2(15)$. But $3\sqrt{3}=\sqrt{27}>4$. So option (d) is the only one that's less than 4.

The answer is (d).


Extension

  • We've seen above that for $0<\alpha <1$, the smallest is (a). For $\alpha>1$, it turns out that $\alpha^{-3}$ is the smallest.
  • $(8!)^9=(8!)^8\times 8!$ and $(9!)^8=(8!)^8\times 9^8$. Now $9^8$ is clearly larger than $8!$ (each is the product of eight things, and in the case of $9^8$, each of those eight things is larger!). So $(9!)^8>(8!)^9$.
     
Last updated on 5 Jul 2024, 10:17am. Please contact us with feedback and comments about this page.