Solutions

Part of the Oxford MAT Livestream

These are the solutions for the Logarithms and powers worksheet.

Warm-up

1. Simplify $(2^3)^4$ and $(2^4)^3$ and $2^42^3$ and $2^32^4$.
   • $(2^3)^4=2^{12}$. $(2^4)^3=2^{12}$. $2^4 2^3=2^7$. $2^3 2^4=2^7$.
2. Solve $x^{-2}+4x^{-1}+3=0$.
   • This is a quadratic for $\frac{1}{x}$ with solutions $\frac{1}{x}=-1$ or $\frac{1}{x}=-3$.
   • So $x=-1$ or $x=-\frac{1}{3}$.
   • Alternatively, we could multiply both sides by $x^2$ and solve the quadratic that we get.
3. Solve $\log_x (x^2)=x^3$.
   • The left-hand side is just $2$ so we want $2=x^3$.
   • So $x=\sqrt[3]{2}$.
4. Solve $log_{x+5}(6x+22)=2$.
   • Take $(x+5)$ to the power of each side to get $6x+22=(x+5)^2$.
   • Expand the square and rearrange for $x^2+4x+3=0$.
   • The solutions are $x=-1$ or $x=-3$.
   • Check these solutions; $\log_4(16)=2$ and $\log_2(4)=2$.
5. Simplify $\log_{10} 3+\log_{10} 4$ into a single term.
   • This is $\log_{10} 12$.
6. Let $a=\ln 2$ and $b=\ln 5$. Write the following in terms of $a$ and $b$.\[\ln 1024, \quad \ln 40, \quad \ln \sqrt{\frac{2}{5}}, \quad \ln \frac{1}{10}, \quad\ln 1.024.\]
   • $\ln 1024=\ln\left(2^{10}\right)=10\ln 2=10a$.
   • $\ln 40=\ln 8+\ln 5=3a+b$.
   • $\ln \sqrt{2/5}=\frac{1}{2}\ln 2/5=\frac{1}{2}\left(a-b\right)$.
   • $\ln (1/10)=-\ln 10=-\ln2-\ln 5=-a-b$.
   • $\ln 1.024=\ln 1024+\ln 1/1000=10a +3(-a-b)=7a-3b$.
   • There are other solutions, partly because $b=a\times\log_2 5$.
7. Expand $\left(e^x+e^{-x}\right)\left(e^y-e^{-y}\right)+\left(e^x-e^{-x}\right)\left(e^y+e^{-y}\right)$.
   • $e^{x+y}+e^{y-x}-e^{x-y}-e^{-x-y}+e^{x+y}-e^{y-x}+e^{x-y}-e^{-x-y}$.
   • That's $2e^{x+y}-2e^{-x-y}$.
8. Expand $\left(e^x+e^{-x}\right)\left(e^y+e^{-y}\right)+\left(e^x-e^{-x}\right)\left(e^y-e^{-y}\right)$.
   • $e^{x+y}+e^{y-x}+e^{x-y}+e^{-x-y}+e^{x+y}-e^{y-x}-e^{x-y}+e^{-x-y}$.
   • That's $2e^{x+y}+2e^{-x-y}$.
9. Solve $2^x=3$. Solve $0.5^x=3$. Solve $4^x=3$.
   • $2^x=3$ is what it means for $x$ to be $\log_2 3$.
   • If $0.5^x=3$ then $2^{-x}=3$ so $x=-\log_2 3$. Alternatively, just write down $x=\log_{0.5}3$.
   • If $4^x=3$ then $2^{2x}=3$ so $x=\frac{1}{2}\log_2 3$. Alternatively, just write down $x=\log_4 3$.
10. For which values of $x$ (if any) does $1^x=1$? For which values of $x$ (if any) does $1^x=3$?
    • $1^x=1$ is true for all real $x$.
    • $1^x$ is never equal to 3 for real $x$.
11. For which values of $b$ (if any) does $0^b=0$? For which values of $a$ (if any) does $a^0=0$?
    • $0^b=0$ for any real $b>0$.
    • $a^0$ is never $0$.

MAT questions

MAT 2015 Q1H

• That's a very strange logarithm. The only way I can think of to get rid of it is to write \[4-5x^2-6x^3=(x^2+2)^2.\]
• Now this is a polynomial question (but we should be careful to go back and check our solutions in the original equation).
• The polynomial rearranges to $x^4+6x^3+9x^2=0$.
• Either $x=0$ or $x^2+6x+9=0$ which has a repeated root $x=-3$.
• Let's quickly check these solutions $\log_2(4)=2$ and $\log_{11}(4-45+162)=\log_{11}121=2$.
• There are two distinct solutions.
• The answer is (c).

MAT 2017 Q1I

• Let's simplify each term. $\log_b\left(\left(b^x\right)^x\right)=x\log_b \left(b^x\right)=x^2\log_b b =x^2$.
• Also, $\log_a\left(\frac{c^x}{b^x}\right)=x\log_a(c/b)=x\left(\log_a c-\log_a b\right)$.
• And the last term is $-\log_a b\log_a c$.
• So this is a quadratic. Even better, we can factorise it \[x^2+\left(\log_a c-\log_a b\right)x-\log_a b\log_a c=\left(x-\log_a b\right)\left(x+\log_a c\right).\]
• Those roots are the same number if $\log_a b=-\log a_c$, which happens when $c=1/b$.
• The answer is (d).

MAT 2013 Q1F

• The only way that we can have $\log_b a=2$ is if $a=b^2$. Similarly, we must have $c-3=b^3$ and $c+5=a^2$.
• These simultaneous equations aren't linear, but we can do our best to solve them.
• For example, we must have $c+5=b^4$ and $c-3=b^3$, so $b^4-b^3=8$. How many solutions does that have?
• Let's sketch $b^3(b-1)$ for $b>0$ (since we're told that $b$ is positive).

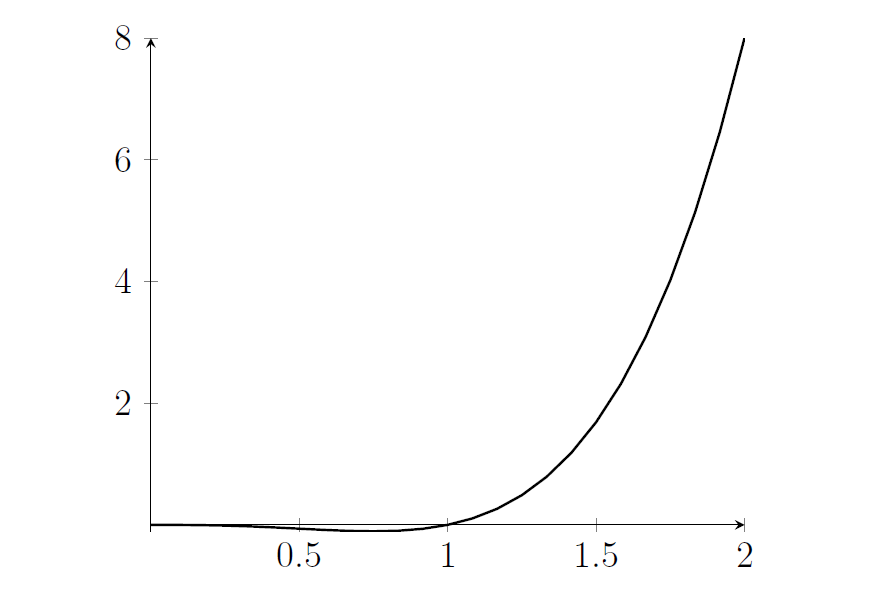
• This is negative in between $0$ and $1$ and then after that it's positive and increases (because $(b-1)$ and $b^3$ are both increasing functions). It can only have one solution for $b^3(b-1)=8$. In fact, that solution is $b=2$, but what we're interested in for this question is that that's a unique solution.
• Now look back at the other equations. We've got $a=b^2=4$ and $c=3+b^3=11$. Let's check the original logarithms. \[ \log_2 4=2,\qquad \log_2 (11-3)=3,\qquad \log_4 (11+5)=2\]
• These equations specify $a$ uniquely (it's 4).
• The answer is (a).

MAT 2013 Q1J

• This is some new notation. It appears in the question in the expression $[2^x]$, which mean the largest integer less than or equal to $2^x$.
• When $x=0$, the term $[2^x]$ is 1. It stays at 1 until we get to a point with $2^x=2$, because then the largest integer less than or equal to $2^x$ will be 2 instead. That happens when $x=1$. Then $2^x$ keeps increasing, but the largest integer under it is still 2, until we get to a point with $2^x=3$.
• Time for a logarithm; that happens when $x=\log_2 3$. There's a pattern here; the function takes each value between 1 and $2^{n-1}$ (it doesn't quite get to $2^n$ until right at the end of the interval when $x=n$).

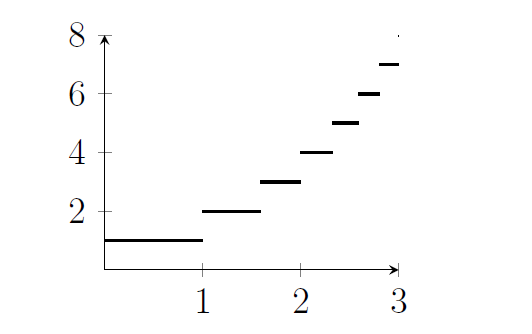
• When we integrate this function from 0 to $n$, we're calculating the area under the graph. That's made of a series of rectangles, and the sum of the areas of those rectangles is \[ 1+(\log_2 3-1)\times 2+ (\log_2 4-\log_2 3)\times 3 +(\log_2 5-\log_2 4)\times 4+\dots + (n-\log_2(2^n-1))\times \left(2^n-1\right) \]
• There's a pattern here (add some $\log_2 k$ then subtract slightly more $\log_2 k$) and it simplifies to \[ -1-\log_2 3-\log_2 4-\dots -\log_2 (2^n-1)+n(2^n-1)\]
• That's $-\log_2\left(\left(2^n-1\right)!\right)+n\left(2^n-1\right)$ which is not quite one of the options.
• But $\log_2 2^n=n$ so we can re-write this as $-\log_2 \left(\left(2^n\right)!\right)+n2^n$.
• The answer is (b).

Reflection

• I really like logarithms, but in lots of these questions getting rid of the logarithm is a good thing to do!
• In that last question, we simplified things by using laws of logarithms and also by using the $k!$ notation for $k\times(k-1)\times\dots\times 2\times1$, which is a very compact way to write that product.