Solutions
Part of the Oxford MAT Livestream
These are the solutions for the Trigonometry worksheet. Don't look at them unless you've had a really good go at the questions, remembering that one of the key skills you're practising is the process of getting stuck and un-stuck on tough questions.
Warm-up
1. Write down the values of $\sin x$ and $\cos x$ and (where possible) $\tan x$ when $x$ is equal to $0^\circ$, $30^\circ$, $45^\circ$, $60^\circ$, $90^\circ$, $120^\circ$, $135^\circ$, $150^\circ$, $180^\circ$, $210^\circ$, $225^\circ$, $240^\circ$, $270^\circ$, $300^\circ$, $315^\circ$, $330^\circ$.
| $0^\circ$ | $30^\circ$ | $45^\circ$ | $60^\circ$ | $90^\circ$ | $120^\circ$ | $135^\circ$ | $150^\circ$ | ... | |
| $\sin x$ | $0$ |
$\frac{1}{2}$ |
$\frac{\sqrt{2}}{2}$ | $\frac{\sqrt{3}}{2}$ | $1$ | $\frac{\sqrt{3}}{2}$ | $\frac{\sqrt{2}}{2}$ | $\frac{1}{2}$ | ... |
| $\cos x$ | $1$ | $\frac{\sqrt{3}}{2}$ | $\frac{\sqrt{2}}{2}$ | $\frac{1}{2}$ | $0$ | $-\frac{1}{2}$ | $-\frac{\sqrt{2}}{2}$ | $-\frac{\sqrt{3}}{2}$ | ... |
| $\tan x$ | $0$ | $\frac{\sqrt{3}}{3}$ | $1$ |
$\sqrt{3}$ |
* |
$-\sqrt{3}$ |
$-1$ | $-\frac{\sqrt{3}}{3}$ | ... |
| $180^\circ$ | $210^\circ$ | $225^\circ$ | $240^\circ$ | $270^\circ$ | $300^\circ$ | $315^\circ$ | $330^\circ$ | $360^\circ$ | |
| $\sin x$ | $0$ | $-\frac{1}{2}$ | $-\frac{\sqrt{2}}{2}$ | $-\frac{\sqrt{3}}{2}$ | $-1$ | $-\frac{\sqrt{3}}{2}$ | $-\frac{\sqrt{2}}{2}$ | $-\frac{1}{2}$ | $0$ |
| $\cos x$ | $-1$ | $-\frac{\sqrt{3}}{2}$ | $-\frac{\sqrt{2}}{2}$ | $-\frac{1}{2}$ | $0$ | $\frac{1}{2}$ | $\frac{\sqrt{2}}{2}$ | $\frac{\sqrt{3}}{2}$ | $1$ |
| $\tan x$ | $0$ | $\frac{\sqrt{3}}{3}$ | $1$ | $\sqrt{3}$ | * | $-\sqrt{3}$ | $-1$ | $-\frac{\sqrt{3}}{3}$ | $0$ |
* $\tan x$ is not defined at $90^\circ$ or $270^\circ$.
2. Find all the solutions to $\displaystyle \sin x = \frac{1}{2}$ with $0\leq x < 360^\circ$.
- From the graph of $\sin x$, we expect two solutions in that range. If I draw a little triangle with opposite side 1 and hypotenuse 2 then I recognise this as half an equilateral triangle (so one solution is $30^\circ$, then using $\sin(180^\circ-x)=\sin x$ another is $150^\circ$). Alternatively, remember the values in the table above.
3. Find all the solutions to $\tan x = 1$ with $0\leq x < 360^\circ$.
- From the graph of $\tan x$, we expect solutions to be $45^\circ+180^\circ n$ for any whole number $n$. In the given range, this is $x=45^\circ$ or $x=225^\circ$.
4. Find all the solutions to $\tan (45x) = 1$ with $0\leq x < 360^\circ$.
- If we write $u=45x$ then we've got $\tan (u)=1$ so $u=45^\circ+180^\circ n$ just like in the previous part. But careful, because if $45x=45^\circ+180^\circ n$ then $x=1^\circ + 4^\circ n$, so the solutions are the angles $1^\circ, 5^\circ, 9^\circ,\dots,357^\circ$, not just $1^\circ$ and $5^\circ$.
5. Write $\left(\cos x + \sin x\right)^2$ in terms of the variable $u=\cos x \sin x$.
- First I can expand the square to get $\cos^2 x + 2\cos x \sin x + \sin^2 x$.
- Now I can use $\cos^2 x+ \sin^2 x=1$ and I can write $2\cos x \sin x$ as $2u$.
- So the expression is $2u+1$.
6. For $0\leq x<90^\circ$, write $1-\sin^2 x+\sin^4 x-\sin^6 x+\dots$ as a single expression (not an infinite sum) in terms of $\cos x$. Why have I excluded $90^\circ$ from the range here?
- This is a geometric series with first term $a=1$ and common ratio $r=-\sin^2x$, so the sum to infinity is $(1+\sin^2 x)^{-1}$ which is $(2-\cos^2 x)^{-1}$ in terms of $\cos x$.
- The sum only converges if the common ratio $r$ satisfies $|r|<1$. This is not the case if $x=90^\circ$.
7. Write $\cos^4x+\cos^2x$ in terms of $\sin x$.
- I'll use $\cos^2 x=1-\sin^2 x$ and substitute this into the expression.
- $\cos^4x+\cos^2x=(1-\sin^2 x)^2+(1-\sin^2 x)=2-3\sin^2 x+\sin^4 x$.
8. Simplify $\cos(450^{\circ} -x)$.
- $\cos(450^\circ-x)=\cos(90^\circ-x)$ using the fact that $\cos x$ is periodic with period $360^\circ$.
- Then $\cos(90^\circ-x)=\sin x$.
9. Simplify $\cos(90^\circ-x)\sin (180^\circ-x)-\sin(90^\circ-x)\cos(180^\circ -x)$.
- We can use $\cos(90^\circ-x)=\sin x$ and $\sin(90^\circ-x)=\cos x$, and also $\sin(180^\circ-x)=\sin x$ and $\cos(180^\circ -x)=-\cos x$.
- We have $(\sin x)(\sin x)-(\cos x)(-\cos x)=\sin^2 x+\cos^2 x=1$.
10. A triangle $ABC$ has side lengths $AB=3$ and $BC=2$, and the angle $\angle ABC=120^\circ$. Find the remaining side length $AC$, the area of the triangle, and an expression for $\sin \angle BCA$.
- Use the cosine rule: $|AC|^2=3^2+2^2-2\times 3 \times 2 \times \cos 120^\circ$, so $|AC|=\sqrt{19}$.
- Use the $\frac{1}{2}ab\sin \gamma$ formula for the area: $\frac{1}{2}\times 3 \times 2 \times \sin 120^\circ=\frac{3\sqrt{3}}{2}$.
- Use the sine rule: $\frac{\sin 120^\circ}{\sqrt{19}}=\frac{\sin \angle BCA}{3}$ so $\sin\angle BCA=\frac{3\sqrt{3}}{2\sqrt{19}}$
11. From the cosine rule, and the fact that $-1\leq \cos \alpha\leq 1$, deduce that for any triangle with side lengths $a>b>c>0$, we must have $a<b+c$.
- The cosine rule is $a^2=b^2+c^2-2bc\cos \alpha$.
- Since $-1\leq \cos \alpha\leq 1$, we have $b^2-2bc+c^2\leq b^2+c^2-2bc\cos \alpha\leq b^2+2bc+c^2$.
- So $(b-c)^2\leq a^2 \leq (b+c)^2$. Since $a>0$ and $(b+c)>0$, it follows that $a\leq b+c$.
- In fact, we can't actually have $a=b+c$ because that would be a triangle with a $180^\circ$ angle. So $a<b+c$.
MAT questions
MAT 2017 Q1B
- This function involves $\cos^2 x$ and $\cos^4 x$. I know a fact about $\cos^2x$ (it's $1-\sin^2 x$) but I can't see an advantage to switching to $\sin^2 x$ here.
- Instead, I'll write it as $f(x)=9(\cos^2 x)^2 - 12 (\cos^2 x)+7$. That looks a bit like a quadratic, and thinking about minimum values makes me think about completing the square (or maybe differentiating a quadratic to find the minimum).
- $f(x)=(3\cos^2x -2)^2+3$. This looks good - I can see that this is definitely bigger than or equal to 3. Can it be as small as 3? That would be when $\cos^2 x=2/3$, which does happen (not for a nice value of $x$, but I know that $\cos^2x$ varies between 0 and 1).
- So the minimum of the function is 3.
- The answer is (a).
MAT 2016 Q1D
- If I write $u=\cos^n x$ then this turns into a quadratic equation $u+u^2=0$, which has solutions $u=0$ or $u=-1$. But let's be careful; we're asked how many solutions there are for $x$, not how many solutions there are for $u$ (the variable we just invented).
- If $u=0$ then $\cos^n x=0$. That happens if and only if $\cos x=0$, for any $n\geq 1$. The solutions to that equation in the given range are $90^\circ$ and $270^\circ$.
- If $u=-1$ then $\cos^n x=-1$. That's impossible if $n$ is even, but if $n$ is odd then it's equivalent to $\cos x =-1$. The only solution to that equation in the given range is $180^\circ$.
- So we have two solutions if $n$ is even, and three solutions if $n$ is odd.
- The answer is (d).
MAT 2017 Q1F
- There are two inequalities here; $\tan x< \cos x$ and $\cos x < \sin x$.
- Drawing graphs, we see that $\cos x<\sin x$ if $45^\circ<x<225^\circ$.
- I would draw graphs of $\cos x$ and $\tan x$ to explore the other inequality in that range.
- For $45^\circ<x<90^\circ$, $\tan x>1$ and so $\tan x>\cos x$. That changes at $90^\circ$, when suddenly $\tan x$ is very negative and the first inequality in the question true. As we increase $x$ further, we reach a point where $\tan x=\cos x$ at some point between $90^\circ$ and $180^\circ$ and then $\tan x>\cos x$ all the way up to $270^\circ$.
- So both inequalities are true from $90^\circ$ to some point between $90^\circ$ and $180^\circ$.
- The answer is (c).
MAT 2013 Q4
(i) For the function \[f(x)=\frac{a+x}{a-x}\] I would check the value at $x=0$ (we have $f(0)=1$)and the behaviour near $x=-a$ (we have $f(-a)=0$) and near $x=a$ (the function gets really big near $x=a$).
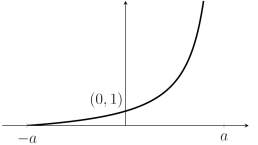
If I did some algebra, I would find that \[f(x)=\frac{a+x}{a-x}=\frac{2a}{a-x}-1\] which is a translation, then a reflection, then a stretch, then a translation of $y=1/x$, so I'd expect the graph to look quite a bit like $y=1/x$.
(ii) If we draw in the radii, then we can split the region $A$ into a sector of a circle and two triangles. This is good because we've got a strategy for finding the area of triangles and the area of sectors of circles. But first we need to find the angles in the triangles. We know that the radius is 1 (so the hypotenuse of each right-angled triangle is 1). For the triangle on the left, we know that the side along the $x$-axis has size $\cos \theta$. That makes the angle at the origin $\theta$. In the other triangle, the side along the $x$-axis has size $\sin \theta$, so this is "opposite" $\theta$, and we should mark in the angle opposite this side as $\theta$.
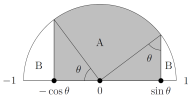
We've got to find the area of each triangle (not too bad because we know that each has sides $\cos \theta$ and $\sin \theta$), and we want the sector of the circle. Brilliantly, the angles at the origin work out so that the sector is one-quarter of a circle (the angle at the centre is $90^\circ$). So the area of $A$ is \(\frac{\pi}{4}+\sin\theta\cos\theta\).
(iii) The relationship between $\sin^2\theta$, $\cos^2\theta$, and $\sin\theta\cos\theta$ is that they're all things that come up when you square $(\sin\theta+\cos\theta)$. Squares are positive so $\sin^2\theta+2\sin\theta\cos\theta+\cos^2\theta\geq 0$. Now substitute in $\sin^2\theta+\cos^2\theta=1$ and rearrange... wait a minute, I've proved that $\sin\theta\cos\theta \geq -\frac{1}{2}$. That's not what I wanted! After checking my work for minus sign errors, I realise that I could instead make these things by squaring $(\sin\theta-\cos\theta)$; that would give me $\sin^2\theta-2\sin\theta\cos\theta+\cos^2\theta\geq 0$ which rearranges to $\sin\theta\cos\theta\geq \frac{1}{2}$.
(iv) We can make this fraction big by making $A$ large and $B$ small. Since $A+B$ is fixed, these things both happen at the same time, and since $A=\frac{\pi}{4}+\sin\theta\cos\theta$, we know from the previous part that it's maximised when $\sin\theta\cos\theta=\frac{1}{2}$ (this happens for $\theta=45^\circ$). At that value of $\theta$, $A$ is $\frac{\pi}{4}+\frac{1}{2}$ and $B$ is $\frac{\pi}{2}-A=\frac{\pi}{4}-\frac{1}{2}$, and the fraction in the question is \[\frac{\pi+2}{\pi-2}.\]
Reflection
- In the long MAT question, I accidentally proved that $\sin\theta\cos\theta\geq-\frac{1}{2}$, which is true but not the thing in the question. Don't give up if this happens to you; maybe you can modify your proof or starting conditions to get to the thing you want.
- We had to sketch a curve in the long MAT question. There's a session coming up (the one after next) where we'll look at more strategies for sketching a curve.
- In the multiple-choice question with the inequalities, it was helpful (helpful to me at least) to split the range into different sections where I could say something in particular about $\tan x$ in each section.
- The other two multiple-choice MAT question had a function that was secretly a quadratic when expressed in terms of a different variable (for example, we could write $u=\cos^2x$ in first question). Spotting the quadratic was good, because it meant that we got to use our knowledge of quadratics. But we've got to be careful when we check the consequences for the original variable. Things would have been quite different if the function had turned out to be $(2\cos^2x -3)^2+3$, because the term inside the brackets is never zero (it's $-1$ or less).

