Half planar random maps
Abstract
Abstract: We study measures on half planar maps that satisfy a natural domain Markov property. I will discuss their classification and some of their geometric properties. Joint work with Gourab Ray.
14:15
Reductions with reduced supersymmetry in generalized geometry
Abstract
16:00
A structural approach to pricing credit default swaps with credit and debt value adjustments
Abstract
A multi-dimensional extension of the structural default model with firms' values driven by diffusion processes with Marshall-Olkin-inspired
correlation structure is presented. Semi-analytical methods for solving
the forward calibration problem and backward pricing problem in three
dimensions are developed. The model is used to analyze bilateral counter- party risk for credit default swaps and evaluate the corresponding credit and debt value adjustments.
Shocking models of meltwater plumes under ice shelves
Abstract
In many places, the Antarctic and Greenland ice sheets are fringed by tongues of ice floating on the ocean, called ice shelves. Recent observations and modelling suggest that melting and disintegration of the floating ice shelves can impact ice sheet flow, and hence have consequences for sea level rise. Of particular interest are observations of channels and undulations in the ice shelf base, for which the conditions for genesis remain unclear. To build insight into the potential for melting-driven instability of the ice shelf base, this talk will consider a free boundary problem with melting at the ice-ocean interface coupled to a buoyant plume of meltwater confined below a stationary ice shelf. An asymptotic model of turbulent heat transfer in the meltwater plume reveals that melting rates depend on ice-shelf basal slope, with potentially shocking consequences for the evolving ice-shelf geometry
p-adic functoriality for inner forms of unitary groups.
Abstract
In this talk I will explain a notion of p-adic functoriality for inner forms of definite unitary groups. Roughly speaking, this is a morphism between so-called eigenvarieties, which are certain rigid analytic spaces parameterizing p-adic families of automorphic forms. We will then study certain properties of classical Langlands functoriality that allow us to prove p-adic functoriality in some "stable" cases.
Moving at the air-water interface
Abstract
It is generally believed that in order to generate waves, a small object (like an insect) moving at the air-water surface must exceed the minimum wave speed (about 23 centimeters per second). We show that this result is only valid for a rectilinear uniform motion, an assumption often overlooked in the literature. In the case of a steady circular motion (a situation of particular importance for the study of whirligig beetles), we demonstrate that no such velocity threshold exists and that even at small velocities a finite wave drag is experienced by the object. This wave drag originates from the emission of a spiral-like wave pattern. The results presented should be important for a better understanding of the propulsion of water-walking insects. For example, it would be very interesting to know if whirligig beetles can take advantage of such spirals for echolocation purposes.
From Borel to Yu (via Gromov): topology via geometric group theory
Abstract
The Borel conjecture is one of the most important (and difficult) conjectures in Topology. We explain how some weaker but highly related conjectures are being tackled through the coarse geometry of finitely generated groups.
Cocycle twists of tensor categories and of rational Cherednik algebras
Abstract
Central extensions of a finite group G correspond to 2-cocycles on G, which give rise to an abelian cohomology group known as the Schur
multiplier of G. Recently, the Schur multiplier was defined in a much more
general setting of a monoidal category. I will explain how to twist algebras by categorical 2-cocycles and will mention the role of
such twists the theory of quantum groups. I will then describe an approach to twisting rational Cherednik algebras by cocycles,
and will discuss possible applications of this new construction to the representation theory of these algebras.
A hybrid finite element-Lagrangian marker technique for geodynamics: Spatial discretisations, implicit solvers and numerics
Abstract
Over million year time scales, the evolution and deformation of rocks on Earth can be described by the equations governing the motion of a very viscous, incompressible fluid. In this regime, the rocks within the crust and mantle lithosphere exhibit both brittle and ductile behaviour. Collectively, these rheologies result in an effective viscosity which is non-linear and may exhibit extremely large variations in space. In the context of geodynamics applications, we are interested in studying large deformation processes both prior and post to the onset of material failure.
\\
\\
Here I introduce a hybrid finite element (FE) - Lagrangian marker discretisation which has been specifically designed to enable the numerical simulation of geodynamic processes. In this approach, a mixed FE formulation is used to discretise the incompressible Stokes equations, whilst the markers are used to discretise the material lithology.
\\
\\
First I will show the a priori error estimates associated with this hybrid discretisation and demonstrate the convergence characteristics via several numerical examples. Then I will discuss several multi-level preconditioning strategies for the saddle point problem which are robust with respect to both large variations in viscosity and the underlying topological structure of the viscosity field.
\\
Finally, I will describe an extension of the multi-level preconditioning strategy that enables high-resolution, three-dimensional simulations to be performed with a small memory footprint and which is performant on multi-core, parallel architectures.
Volatility Estimation Using Flat-Top Realized Kernels
Abstract
This paper analyzes a generalized class of flat-top realized kernels for
estimation of the quadratic variation spectrum in the presence of a
market microstructure noise component that is allowed to exhibit both
endogenous and exogenous $\alpha$-mixing dependence with polynomially
decaying autocovariances. In the absence of jumps, the class of flat-top
estimators are shown to be consistent, asymptotically unbiased, and
mixed Gaussian with the optimal rate of convergence, $n^{1/4}$. Exact
bounds on lower order terms are obtained using maximal inequalities and
these are used to derive a conservative MSE-optimal flat-top shrinkage.
In a theoretical and/or a numerical comparison with alternative
estimators, including the realized kernel, the two-scale realized
kernel, and a proposed robust pre-averaging estimator, the flat-top
realized kernels are shown to have superior bias reduction properties
with little or no increase in finite sample variance.
The pullback equation for differential forms
Abstract
{\bf This seminar is at ground floor!}
\\
An important question in geometry and analysis is to know when two $k-$forms
$f$ and $g$ are equivalent. The problem is therefore to find a map $\varphi$
such that%
\[
\varphi^{\ast}\left( g\right) =f.
\]
We will mostly discuss the symplectic case $k=2$ and the case of volume forms
$k=n.$ We will give some results when $3\leq k\leq n-2,$ the case $k=n-1$ will
also be considered.
\\
The results have been obtained in collaboration with S. Bandyopadhyay, G.
Csato and O. Kneuss and can be found, in part, in the book below.\bigskip
\\
\newline
Csato G., Dacorogna B. et Kneuss O., \emph{The pullback equation for
differential forms}, Birkha\"{u}ser, PNLDE Series, New York, \textbf{83} (2012).
11:00
Model Theory of Adeles, Adele Classes, and Residual Hyperfields of Valued Fields
Abstract
This is joint work with Angus Macintyre. We study model-theoretic properties of
the ring of adeles, the hyperring of adele classes (studied by Connes-Consani),
and residual hyperfields of valued fields (in the sense of Krasner).
Cubulating small cancellation and random groups
Abstract
I'll discuss work of Wise and Ollivier-Wise that gives cubulations of certain small cancellation and random groups, which in turn shows that they do not have property (T).
10:30
Flexagons
Abstract
There appears to be no universally accepted rigorous definition of a "flexagon" (although I will try to give a reasonable one in the talk). Examples of flexagons were most likely discovered and rediscovered many times in the past - but they were "officially" discovered in 1939, a serendipitous consequence of the discrepancy between US paper sizes and sensible paper sizes.* I'll describe a couple of the most famous examples of flexagons (with actual models to play with of course), and also introduce some of the more abstract theory of flexagons which has been developed. Feel free to bring your own models of flexagons!
* The views expressed herein are solely those of the speaker, and do not reflect the official position of the Kinderseminar w.r.t. international paper standards.
Dielectrowetting driven spreading of droplets and shaping of liquid interfaces
Abstract
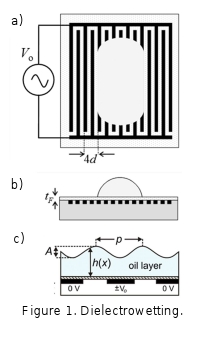 The contact angle of a
liquid droplet on a surface can be controlled by making the droplet part of a
capacitive structure where the droplet contact area forms one electrode to
create an electrowetting-on-dielectric (EWOD) configuration [1]. EWOD
introduces a capacitive energy associated with the charging of the solid-liquid
interface, in addition to the surface free energy, to allow the contact angle,
and hence effective hydrophilicity of a surface, to be controlled using a voltage.
However, the substrate must include an electrode coated with a thin, and
typically hydrophobic, solid insulating layer and the liquid must be
conducting, typically a salt solution, and have a direct electrical contact. In
this seminar I show that reversible voltage programmed control of droplet
wetting of a surface can be achieved using non-conducting dielectric liquids
and without direct electrical contact. The approach is based on non-uniform
electric fields generated via interdigitated electrodes and liquid
dielectrophoresis to alter the energy balance of a droplet on a solid surface
(Fig. 1a,b). Data is shown for thick droplets demonstrating the change in the
cosine of the contact angle is proportional to the square of the applied
voltage and it is shown theoretically why this equation, similar to that found
for EWOD can be expected [2]. I also show that as the droplet spreads and
becomes a film, the dominant change in surface free energy to be expected occurs
by a wrinkling/undulation of the liquid-vapor interface (Fig. 1c) [3,4]. This
type of wrinkle is shown to be a method to create a voltage programmable phase
grating [5]. Finally, I argue that dielectrowetting can be used to modify the
dynamic contact angle observed during droplet spreading and that this is
described by a modified form of the Hoffman-de Gennes law for the relationship
between edge speed and contact angle. In this dynamic situation, three distinct
regimes can be predicted theoretically and are observed experimentally. These
correspond to an exponential approach to equilibrium, a pure Tanner’s law type
power law and a voltage determined superspreading power law behavior [6].
The contact angle of a
liquid droplet on a surface can be controlled by making the droplet part of a
capacitive structure where the droplet contact area forms one electrode to
create an electrowetting-on-dielectric (EWOD) configuration [1]. EWOD
introduces a capacitive energy associated with the charging of the solid-liquid
interface, in addition to the surface free energy, to allow the contact angle,
and hence effective hydrophilicity of a surface, to be controlled using a voltage.
However, the substrate must include an electrode coated with a thin, and
typically hydrophobic, solid insulating layer and the liquid must be
conducting, typically a salt solution, and have a direct electrical contact. In
this seminar I show that reversible voltage programmed control of droplet
wetting of a surface can be achieved using non-conducting dielectric liquids
and without direct electrical contact. The approach is based on non-uniform
electric fields generated via interdigitated electrodes and liquid
dielectrophoresis to alter the energy balance of a droplet on a solid surface
(Fig. 1a,b). Data is shown for thick droplets demonstrating the change in the
cosine of the contact angle is proportional to the square of the applied
voltage and it is shown theoretically why this equation, similar to that found
for EWOD can be expected [2]. I also show that as the droplet spreads and
becomes a film, the dominant change in surface free energy to be expected occurs
by a wrinkling/undulation of the liquid-vapor interface (Fig. 1c) [3,4]. This
type of wrinkle is shown to be a method to create a voltage programmable phase
grating [5]. Finally, I argue that dielectrowetting can be used to modify the
dynamic contact angle observed during droplet spreading and that this is
described by a modified form of the Hoffman-de Gennes law for the relationship
between edge speed and contact angle. In this dynamic situation, three distinct
regimes can be predicted theoretically and are observed experimentally. These
correspond to an exponential approach to equilibrium, a pure Tanner’s law type
power law and a voltage determined superspreading power law behavior [6].
Acknowledgements
GM acknowledges the contributions of colleagues Professor Carl Brown, Dr. Mike Newton, Dr. Gary Wells and Mr Naresh Sampara at Nottingham Trent University who were central to the development of this work. EPSRC funding under grant EP/E063489/1 is also gratefully acknowledged.
References
[1] F. Mugele and J.C. Baret, “Electrowetting: From basics to applications”, J. Phys.: Condens. Matt., 2005, 17, R705-R774.
[2] G. McHale, C.V. Brown, M.I. Newton, G.G. Wells and N. Sampara, “Dielectrowetting driven spreading of droplets”, Phys. Rev. Lett., 2011, 107, art. 186101.
[3] C.V. Brown, W. Al-Shabib, G.G. Wells, G. McHale and M.I. Newton, “Amplitude scaling of a static wrinkle at an oil-air interface created by dielectrophoresis forces”, Appl. Phys. Lett., 2010, 97, art. 242904.
[4] C.V. Brown, G. McHale and N.J. Mottram, “Analysis of a static wrinkle on the surface of a thin dielectric liquid layer formed by dielectrophoresis forces”, J. Appl. Phys. 2011, 110 art. 024107.
[5] C.V. Brown, G. G. Wells, M.I. Newton and G. McHale, “Voltage-programmable liquid optical interface”, Nature Photonics, 2009, 3, 403-405.
[6] C.V. Brown, G. McHale and N. Sampara, “Voltage induced superspreading of droplets”, submitted (2012)
17:00
"Asymptotics of homology groups in finitely presented residually free groups".
Abstract
One of the applications of the study of assymptotics of
homology groups in residually free groups of type FP_m is the calculation
of their analytic betti numbers in dimension up to m.
Jobs for Mathematicians
Abstract
Exhibitors will be here along with recruiters from different sectors. There will also be panel talks. For further information see http://www.careers.ox.ac.uk/wp-content/uploads/2012/02/JobsForMathemati… and in particular last year brochure for the event at http://www.careers.ox.ac.uk/wp-content/uploads/2012/04/MathsPrintII.pdf
Long paths and cycles in subgraphs of the cube
Abstract
Let $Q_n$ denote the graph of the $n$-dimensional cube with vertex set $\{0, 1\}^n$
in which two vertices are adjacent if they differ in exactly one coordinate.
Suppose $G$ is a subgraph of $Q_n$ with average degree at least $d$. How long a
path can we guarantee to find in $G$?
My aim in this talk is to show that $G$ must contain an exponentially long
path. In fact, if $G$ has minimum degree at least $d$ then $G$ must contain a path
of length $2^d − 1$. Note that this bound is tight, as shown by a $d$-dimensional
subcube of $Q^n$. I hope to give an overview of the proof of this result and to
discuss some generalisations.
Rough Solutions of Einstein Vacuum equations in CMCSH gauge
Abstract
I will report my work on rough solutions to Cauchy problem for the Einstein vacuum equations in CMC spacial harmonic gauge, in which we obtain the local well-posedness result in $H^s$, $s$>$2$. The novelty of this approach lies in that, without resorting to the standard paradifferential regularization over the rough, Einstein metric $\bf{g}$, we manage to implement the commuting vector field approach to prove Strichartz estimate for geometric wave equation $\Box_{\bf{g} } \phi=0$ directly. If time allows, I will talk about my work in progress on the sharp results for the more general quasilinear wave equations by vector fields approach.
Balloons and Hoops and their Universal Finite Type Invariant, BF Theory, and an Ultimate Alexander Invariant
Abstract
Balloons are two-dimensional spheres. Hoops are one dimensional loops. Knotted Balloons and Hoops (KBH) in 4-space behave much like the first and second fundamental groups of a topological space - hoops can be composed like in π1, balloons like in π2, and hoops "act" on balloons as π1 acts on π2. We will observe that ordinary knots and tangles in 3-space map into KBH in 4-space and become amalgams of both balloons and hoops.
We give an ansatz for a tree and wheel (that is, free-Lie and cyclic word) -valued invariant ζ of KBHs in terms of the said compositions and action and we explain its relationship with finite type invariants. We speculate that ζ is a complete evaluation of the BF topological quantum field theory in 4D, though we are not sure what that means. We show that a certain "reduction and repackaging" of ζ is an "ultimate Alexander invariant" that contains the Alexander polynomial (multivariable, if you wish), has extremely good composition properties, is evaluated in a topologically meaningful way, and is least-wasteful in a computational sense. If you believe in categorification, that's a wonderful playground.
For further information see http://www.math.toronto.edu/~drorbn/Talks/Oxford-130121/
The stochastic quasi-geostrophic equation
Abstract
prove the existence of martingale solutions and Markov selections for multiplicative noise for all _ 2 (0; 1) . In the subcritical case _ > 1=2, we prove existence and uniqueness of (probabilistically) strong solutions. We obtain the ergodicity for _ > 1=2 for degenerate noise. We also study the long time behaviour of the solutions tothe 2D stochastic quasi-geostrophic equation on T2 driven by real linear multiplicative noise and additive noise in the subcritical case by proving the existence of a random attractor.
Contraction Rates for Bayesian Inverse Problems
Abstract
Abstract: We consider the inverse problem of recovering u from a noisy, indirect observation We adopt a Bayesian approach, in which the aim is to determine the posterior distribution _y on the unknown u, given some prior information about u in the form of a prior distribution _0,together with the observation y. We are interested in the question of posterior consistency, which is the characterization of the behaviour of _y as more data become available. We work in a separable Hilbert space X, assuming a Gaussian prior _0 = N(0; _ 2C0). The theory is developed using two concrete problems: i) a family of linear inverse problems in which we want to _nd u from y where y = A
14:15
Umbral Moonshine
Abstract
16:00
Brownian Motions and Martingales under Probability Model Uncertainty
Abstract
The models of Brownian motion, Poisson processes, Levy processes and martingales are frequently used as basic formulations of prices in financial market. But probability and/or distribution uncertainties cause serious problems of robustness. Nonlinear expectations (G-Expectations) and the corresponding martingales are useful tools to solve them.
Computing the local Cassels-Tate pairing.
Abstract
Let K be a number field and E/K be an elliptic curve. Multiplication by n induces a map from the n^2-Selmer group of E/K to the n-Selmer group. The image of this map contains the image of E(K) in the n-Selmer group and is often smaller. Thus, computing the image of the n^2-Selmer group under multiplication by n can give a tighter bound on the rank of E/K. The Cassels-Tate pairing is a pairing on the n-Selmer group whose kernel is equal to the image of the n^2-Selmer group under multiplication by n. For n=2, Cassels gave an explicit description of the Cassels-Tate pairing as a sum of local pairings and computed the local pairing in terms of the Hilbert symbol. In this talk, I will give a formula for the local Cassels-Tate pairing for n=3 and describe an algorithm to compute it for n an odd prime. This is joint work with Tom Fisher.
Compressed sensing and matrix completion: exploiting simplicity in data
Abstract
The essential information contained in most large data sets is
small when compared to the size of the data set. That is, the
data can be well approximated using relatively few terms in a
suitable transformation. Compressed sensing and matrix completion
show that this simplicity in the data can be exploited to reduce the
number of measurements. For instance, if a vector of length $N$
can be represented exactly using $k$ terms of a known basis
then $2k\log(N/k)$ measurements is typically sufficient to recover
the vector exactly. This can result in dramatic time savings when
k
Useful geometry and modular forms
Abstract
Algebraic geometry has become the standard language for many number theorists in recent decades. In this talk, we will define modular forms and related objects in the language of modern geometers, thereby giving a geometric motivation for their study. We will ask some naive questions from a purely geometric point of view about these objects, and try to answer them using standard geometric techniques. If time permits, we will discuss some rather deep consequences in number theory of our geometric excursion, and mention open problems in geometry whose solution would have profound consequences in number theory.
Multi-task Learning and Structured Sparsity
Abstract
We discuss the problem of estimating a structured matrix with a large number of elements. A key motivation for this problem occurs in multi-task learning. In this case, the columns of the matrix correspond to the parameters of different regression or classification tasks, and there is structure due to relations between the tasks. We present a general method to learn the tasks' parameters as well as their structure. Our approach is based on solving a convex optimization problem, involving a data term and a penalty term. We highlight different types of penalty terms which are of practical and theoretical importance. They implement structural relations between the tasks and achieve a sparse representations of parameters. We address computational issues as well as the predictive performance of the method. Finally we discuss how these ideas can be extended to learn non-linear task functions by means of reproducing kernels.
Auslander-Reiten-quivers in functorially finite resolving subcategories
Abstract
It has been shown that the Auslander-Reiten-quiver of an indecomposable algebra contains a finite component if and only if A is representation finite. Moreover, selfinjective algebras are representation finite if and only if the tree types of the stable components are given by Dynkin Diagrams. I will present similar results for the Auslander-Reiten-quiver of a functorially finite resolving subcategory Ω. We will see that Brauer-Thrall 1 and Brauer-Thrall 1.5 can be proved for these categories with only little extra effort. Furthermore, a connection between sectional paths in A-mod and irreducible morphisms in Ω will be given. Finally, I will show how all finite Auslander-Reiten-quivers of A-mod or Ω are related to Dynkin Diagrams with a notion similar to the tree type that coincides in a finite stable component.
12:00
Relaxation in BV via polyhedral approximation
Abstract
We first provide a brief overview of some of the key properties of the space $\textrm{BV}(\Omega;\mathbb{R}^{N})$ of functions of Bounded Variation, and the motivation for its use in the Calculus of Variations. Now consider the variational integral
\[
F(u;\Omega):=\int_{\Omega}f(Du(x))\,\textrm{d} x\,\textrm{,}
\]
where $\Omega\subset\mathbb{R}^{n}$ is open and bounded, and $f\colon\mathbb{R}^{N\times n}\rightarrow\mathbb{R}$ is a continuous function satisfying the growth condition $0\leq f(\xi)\leq L(1+|\xi|^{r})$ for some exponent $r$. When $u\in\textrm{BV}(\Omega;\mathbb{R}^{N})$, we extend the definition of $F(u;\Omega)$ by introducing the functional
\[
\mathscr{F}(u,\Omega):= \inf_{(u_{j})}\bigg\{ \liminf_{j\rightarrow\infty}\int_{\Omega}f(Du_{j})\,\textrm{d} x\, \left|
\!\!\begin{array}{r}
(u_{j})\subset W_{\textrm{loc}}^{1,r}(\Omega, \mathbb{R}^{N}) \\
u_{j} \stackrel{\ast}{\rightharpoonup} u\,\,\textrm{in }\textrm{BV}(\Omega, \mathbb{R}^{N})
\end{array} \right. \bigg\} \,\textrm{.}
\]
\noindent For $r\in [1,\frac{n}{n-1})$, we prove that $\mathscr{F}$ satisfies the lower bound
\[
\mathscr{F}(u,\Omega) \geq \int_{\Omega} f(\nabla u (x))\,\textrm{d} x + \int_{\Omega}f_{\infty} \bigg(\frac{D^{s}u}{|D^{s}u|}\bigg)\,|D^{s}u|\,\textrm{,}
\]
provided $f$ is quasiconvex, and the recession function $f_{\infty}$ ($:= \overline{\lim}_{t\rightarrow\infty}f(t\xi )/t$) is assumed to be finite in certain rank-one directions. This result is a natural extension of work by Ambrosio and Dal Maso, which deals with the case $r=1$; it involves combining work of Kristensen, Braides and Coscia with some new techniques, including a polyhedral approximation result and a blow-up argument that exploits fine properties of BV functions.
Relations between some topological and group theoretic conjectures
Abstract
I will be looking at some conjectures and theorems closely related to the h-cobordism theorem and will try to show some connections between them and some group theoretic conjectures.
10:30
17:00
Homological dimension of soluble groups and some new complement and supplement theorems.
Abstract
The homological dimension of a group can be computed over any coefficient ring $K$.
It has long been known that if a soluble group has finite homological dimension over $K$
then it has finite Hirsch length and the Hirsch length is an upper bound for the homological
dimension. We conjecture that equality holds: i.e. the homological dimension over $K$ is
equal to the Hirsch length whenever the former is finite. At first glance this conjecture looks
innocent enough. The conjecture is known when $K$ is taken to be the integers or the field
of rational numbers. But there is a gap in the literature regarding finite field coefficients.
We'll take a look at some of the history of this problem and then show how some new near complement
and near supplement theorems for minimax groups can be used to establish the conjecture
in special cases. I will conclude by speculating what may be required to solve the conjecture outright.
14:15
Supersymmetric loop space
Abstract
We will first review the construction of N =1
supersymmetric Yang-Mills theory in three dimensions. Then we will
construct a superloop space formulation for this super-Yang-Mills
theory in three dimensions.Thus, we will obtain expressions for loop
connection and loop curvature in this superloop space. We will also
show that curvature will vanish, unless there is a monopole in the
spacetime. We will also construct a quantity which will give the
monopole charge in this formalism. Finally, we will show how these
results hold even in case of deformed superspace.
N-covering stationary points and constrained variational problems
Abstract
In this talk we show how degree N maps of the form $u_{N}(z) = \frac{z^{N}}{|z|^{N-1}}$ arise naturally as stationary points of functionals like the Dirichlet energy. We go on to show that the $u_{N}$ are minimizers of related variational problems, including one whose associated Euler-Lagrange equation bears a striking resemblance to a system studied by N. Meyers in the 60s, and another where the constraint $\det \nabla u = 1$ a.e. plays a prominent role.

