 The contact angle of a
liquid droplet on a surface can be controlled by making the droplet part of a
capacitive structure where the droplet contact area forms one electrode to
create an electrowetting-on-dielectric (EWOD) configuration [1]. EWOD
introduces a capacitive energy associated with the charging of the solid-liquid
interface, in addition to the surface free energy, to allow the contact angle,
and hence effective hydrophilicity of a surface, to be controlled using a voltage.
However, the substrate must include an electrode coated with a thin, and
typically hydrophobic, solid insulating layer and the liquid must be
conducting, typically a salt solution, and have a direct electrical contact. In
this seminar I show that reversible voltage programmed control of droplet
wetting of a surface can be achieved using non-conducting dielectric liquids
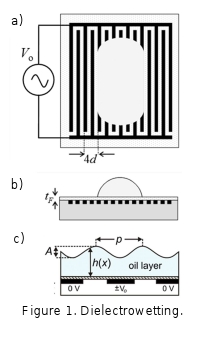
and without direct electrical contact. The approach is based on non-uniform
electric fields generated via interdigitated electrodes and liquid
dielectrophoresis to alter the energy balance of a droplet on a solid surface
(Fig. 1a,b). Data is shown for thick droplets demonstrating the change in the
cosine of the contact angle is proportional to the square of the applied
voltage and it is shown theoretically why this equation, similar to that found
for EWOD can be expected [2]. I also show that as the droplet spreads and
becomes a film, the dominant change in surface free energy to be expected occurs
by a wrinkling/undulation of the liquid-vapor interface (Fig. 1c) [3,4]. This
type of wrinkle is shown to be a method to create a voltage programmable phase
grating [5]. Finally, I argue that dielectrowetting can be used to modify the
dynamic contact angle observed during droplet spreading and that this is
described by a modified form of the Hoffman-de Gennes law for the relationship
between edge speed and contact angle. In this dynamic situation, three distinct
regimes can be predicted theoretically and are observed experimentally. These
correspond to an exponential approach to equilibrium, a pure Tanner’s law type
power law and a voltage determined superspreading power law behavior [6].
The contact angle of a
liquid droplet on a surface can be controlled by making the droplet part of a
capacitive structure where the droplet contact area forms one electrode to
create an electrowetting-on-dielectric (EWOD) configuration [1]. EWOD
introduces a capacitive energy associated with the charging of the solid-liquid
interface, in addition to the surface free energy, to allow the contact angle,
and hence effective hydrophilicity of a surface, to be controlled using a voltage.
However, the substrate must include an electrode coated with a thin, and
typically hydrophobic, solid insulating layer and the liquid must be
conducting, typically a salt solution, and have a direct electrical contact. In
this seminar I show that reversible voltage programmed control of droplet
wetting of a surface can be achieved using non-conducting dielectric liquids
and without direct electrical contact. The approach is based on non-uniform
electric fields generated via interdigitated electrodes and liquid
dielectrophoresis to alter the energy balance of a droplet on a solid surface
(Fig. 1a,b). Data is shown for thick droplets demonstrating the change in the
cosine of the contact angle is proportional to the square of the applied
voltage and it is shown theoretically why this equation, similar to that found
for EWOD can be expected [2]. I also show that as the droplet spreads and
becomes a film, the dominant change in surface free energy to be expected occurs
by a wrinkling/undulation of the liquid-vapor interface (Fig. 1c) [3,4]. This
type of wrinkle is shown to be a method to create a voltage programmable phase
grating [5]. Finally, I argue that dielectrowetting can be used to modify the
dynamic contact angle observed during droplet spreading and that this is
described by a modified form of the Hoffman-de Gennes law for the relationship
between edge speed and contact angle. In this dynamic situation, three distinct
regimes can be predicted theoretically and are observed experimentally. These
correspond to an exponential approach to equilibrium, a pure Tanner’s law type
power law and a voltage determined superspreading power law behavior [6].
Acknowledgements
GM acknowledges the contributions of
colleagues Professor Carl Brown, Dr. Mike Newton, Dr. Gary Wells and Mr Naresh Sampara
at Nottingham Trent University who were central to the development of this
work. EPSRC funding under grant EP/E063489/1 is also gratefully acknowledged.
References
[1] F. Mugele and J.C. Baret, “Electrowetting:
From basics to applications”, J. Phys.:
Condens. Matt., 2005, 17, R705-R774.
[2] G. McHale, C.V. Brown, M.I. Newton, G.G. Wells
and N. Sampara, “Dielectrowetting driven spreading of droplets”, Phys. Rev. Lett., 2011, 107,
art. 186101.
[3] C.V. Brown, W. Al-Shabib, G.G. Wells, G.
McHale and M.I. Newton, “Amplitude scaling of a static wrinkle at an oil-air
interface created by dielectrophoresis forces”, Appl. Phys. Lett., 2010, 97,
art. 242904.
[4] C.V. Brown, G. McHale and N.J. Mottram, “Analysis
of a static wrinkle on the surface of a thin dielectric liquid layer formed by
dielectrophoresis forces”, J. Appl. Phys.
2011, 110 art. 024107.
[5] C.V. Brown, G. G. Wells, M.I. Newton and G.
McHale, “Voltage-programmable liquid optical interface”, Nature Photonics, 2009, 3, 403-405.
[6] C.V. Brown, G. McHale and N. Sampara, “Voltage
induced superspreading of droplets”, submitted (2012)


 The contact angle of a
liquid droplet on a surface can be controlled by making the droplet part of a
capacitive structure where the droplet contact area forms one electrode to
create an electrowetting-on-dielectric (EWOD) configuration [1]. EWOD
introduces a capacitive energy associated with the charging of the solid-liquid
interface, in addition to the surface free energy, to allow the contact angle,
and hence effective hydrophilicity of a surface, to be controlled using a voltage.
However, the substrate must include an electrode coated with a thin, and
typically hydrophobic, solid insulating layer and the liquid must be
conducting, typically a salt solution, and have a direct electrical contact. In
this seminar I show that reversible voltage programmed control of droplet
wetting of a surface can be achieved using non-conducting dielectric liquids
and without direct electrical contact. The approach is based on non-uniform
electric fields generated via interdigitated electrodes and liquid
dielectrophoresis to alter the energy balance of a droplet on a solid surface
(Fig. 1a,b). Data is shown for thick droplets demonstrating the change in the
cosine of the contact angle is proportional to the square of the applied
voltage and it is shown theoretically why this equation, similar to that found
for EWOD can be expected [2]. I also show that as the droplet spreads and
becomes a film, the dominant change in surface free energy to be expected occurs
by a wrinkling/undulation of the liquid-vapor interface (Fig. 1c) [3,4]. This
type of wrinkle is shown to be a method to create a voltage programmable phase
grating [5]. Finally, I argue that dielectrowetting can be used to modify the
dynamic contact angle observed during droplet spreading and that this is
described by a modified form of the Hoffman-de Gennes law for the relationship
between edge speed and contact angle. In this dynamic situation, three distinct
regimes can be predicted theoretically and are observed experimentally. These
correspond to an exponential approach to equilibrium, a pure Tanner’s law type
power law and a voltage determined superspreading power law behavior [6].
The contact angle of a
liquid droplet on a surface can be controlled by making the droplet part of a
capacitive structure where the droplet contact area forms one electrode to
create an electrowetting-on-dielectric (EWOD) configuration [1]. EWOD
introduces a capacitive energy associated with the charging of the solid-liquid
interface, in addition to the surface free energy, to allow the contact angle,
and hence effective hydrophilicity of a surface, to be controlled using a voltage.
However, the substrate must include an electrode coated with a thin, and
typically hydrophobic, solid insulating layer and the liquid must be
conducting, typically a salt solution, and have a direct electrical contact. In
this seminar I show that reversible voltage programmed control of droplet
wetting of a surface can be achieved using non-conducting dielectric liquids
and without direct electrical contact. The approach is based on non-uniform
electric fields generated via interdigitated electrodes and liquid
dielectrophoresis to alter the energy balance of a droplet on a solid surface
(Fig. 1a,b). Data is shown for thick droplets demonstrating the change in the
cosine of the contact angle is proportional to the square of the applied
voltage and it is shown theoretically why this equation, similar to that found
for EWOD can be expected [2]. I also show that as the droplet spreads and
becomes a film, the dominant change in surface free energy to be expected occurs
by a wrinkling/undulation of the liquid-vapor interface (Fig. 1c) [3,4]. This
type of wrinkle is shown to be a method to create a voltage programmable phase
grating [5]. Finally, I argue that dielectrowetting can be used to modify the
dynamic contact angle observed during droplet spreading and that this is
described by a modified form of the Hoffman-de Gennes law for the relationship
between edge speed and contact angle. In this dynamic situation, three distinct
regimes can be predicted theoretically and are observed experimentally. These
correspond to an exponential approach to equilibrium, a pure Tanner’s law type
power law and a voltage determined superspreading power law behavior [6].