Kinetic and Mean-Field Equations

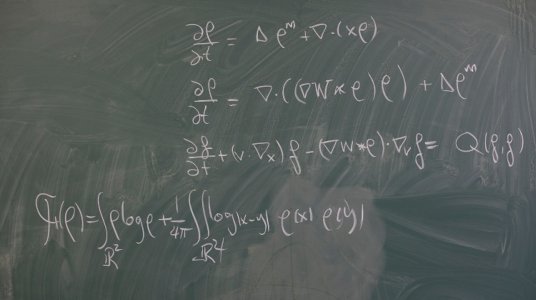
We are interested in Partial Differential Equations arising from probabilistic descriptions of the averaged behavior of large number of "particles". Some classical and modern instances of applications are: molecules in gases, electron transport in semiconductor materials, ions and electrons in plasmas, grains or beads in granular gases, stars or galaxies in astrophysics, chains of molecules in polymer flows, endothelial cells in chemotactic movement for angiogenesis, neurons spike dynamics in neuroscience, fuel droplets in Diesel engines, dust particles in atmospheric pollution, animals in a swarm, agents in an economic market, pedestrians strolling around complex building geometries...

This diversity of applications should not hide the common underlying methods, models and structural equations derived in all of these problems. We are interested in the qualitative behavior of solutions, long time asymptotics, asymptotic limits, well-posedness, and derivation and connections between different levels of description. Some specific topics are:

- Nonlinear nonlocal Fokker-Planck equations. Kinetic-Fluid coupling.
- Collisional kinetic theory: inelastic Boltzmann equation, the Landau equation in plasmas.
- Mean-field limits, asymptotic limits, closures and related hydrodynamical systems and aggregation-diffusion equations.
- Kinetic equations in mathematical biology: computational neuroscience and collective behavior.

Faculty: José A. Carrillo, Gui-Qiang G. Chen and Endre Suli.

Postdoctoral Fellows: Rafael Bailo, Immanuel Ben Porat, Antonio Esposito, Alexandra Holzinger and Jakub Skrzeckowski 

DPhil Students: Andrea Clini, Stefano Fronzoni, Carles Falco I Gandia, Shuchen Guo, Yifan Jiang, Alejandro Fernández Jiménez, Chuhui He, and Jethro Warnett