15:45
Trying to understand mapping class groups of algebraic surfaces from the Thurstonian point of view
Abstract
In some ways the theory of mapping class groups of 4-manifolds is in 2020 at the same place where the theory of mapping class groups of 2-manifolds was in 1973, before Thurston changed everything. In this talk I will describe some first steps in an ongoing joint project with Eduard Looijenga where we are trying to understand mapping class groups of certain algebraic surfaces (e.g. rational elliptic surfaces, and also K3 surfaces) from the Thurstonian point of view.
North Meets South
Abstract
Paolo Aceto
Knot concordance and homology cobordisms of 3-manifolds
We introduce the notion of knot concordance for knots in the 3-sphere and discuss some key problems regarding the smooth concordance group. After defining homology cobordisms of 3-manifolds we introduce the integral and rational homology cobordism groups and briefly discuss their relationship with the concordance group. We conclude stating a few recent results and open questions on the structure of these groups.
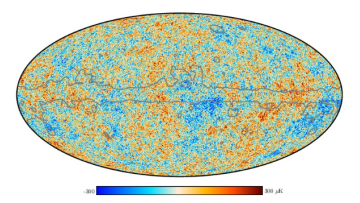
Oxford Mathematicians Dmitry Belyaev and Michael McAuley explain the ubiquitous role of Gaussian Fields in modelling spatial phenomena across science, and especially in cosmology. This case-study is based on work with Stephen Muirhead at Queen Mary University of London (QMUL).
14:15
Quantum K-theory and 3d A-model
Abstract
I will discuss some ongoing work on three-dimensional supersymmetric gauge theories and their relationship to (equivariant) quantum K-theory. I will emphasise the interplay between the physical and mathematical motivations and approaches, and attempt to build a dictionary between the two. As an interesting example, I will discuss the quantum K-theory of flag manifolds. The QK ring will be related to the vacuum structure of a gauge theory with Chern-Simons interactions, and the (genus-0) K-theoretic invariants will be computed in terms of explicit residue formulas that can be derived from the relevant supersymmetric path integrals.
Nebulae