Our latest book features the remarkable story of Ada Lovelace, often considered the world’s first computer programmer, as told in a new book co-written by Oxford Mathematicians Christopher Hollings and Ursula Martin together with colleague Adrian Rice from Randolph-Macon College.
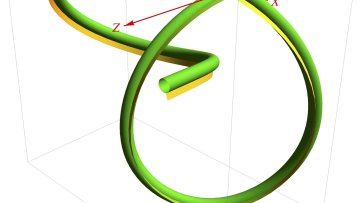
Knots are widespread, universal physical structures, from shoelaces to Celtic decoration to the many variants familiar to sailors. They are often simple to construct and aesthetically appealing, yet remain topologically and mechanically quite complex.
Knots are also common in biopolymers such as DNA and proteins, with significant and often detrimental effects, and biological mechanisms also exist for 'unknotting'.
Mon, 30 Apr 2018
14:15 -
15:15
L4
C^infinity Schemes, and Manifolds with Corners
Kelli Francis-Staite
(Oxford)
Abstract
A C^infinity scheme is a version of a scheme that uses a maximal spectrum. The category of C^infinity schemes contains the category of Manifolds as a full subcategory, as well as being closed under fibre products. In other words, this category is equipped to handle intersection singularities of smooth spaces.
While originally defined in the set up of Synthetic Differential Geometry, C^infinity schemes have more recently been used to describe derived manifolds, for example, the d-manifolds of Joyce. There are applications of this in Symplectic Geometry, such as the describing the moduli space of J-holomorphic forms.
In this talk, I will describe the category of C^infinity schemes, and how this idea can be extended to manifolds with corners. If time, I will mention the applications of this in derived geometry.
Tue, 01 May 2018
12:00 -
13:15
L4
The double copy: from BRST ghosts to black hole solutions
Dr Sylvia Nagy
(Nottingham)
Abstract
I will present a procedure for perturbatively constructing the field content of gravitational theories from a convolutive product of two Yang-Mills theories. A dictionary "gravity=YM * YM" is developed, reproducing the symmetries and dynamics of the gravity theory from those of the YM theories. I will explain the unexpected, yet crucial role played by the BRST ghosts of the YM system in the construction of gravitational fields. The dictionary is expected to develop into a solution-generating technique for gravity.
