High Resolution Computational Wave Flume
 Reseacher: Helen Fletcher
Reseacher: Helen Fletcher- Academic Supervisors: S. Jon Chapman, Philippe Trinh (University of Bath) and Jonathan Whiteley
- Industrial Supervisors: Christopher Kees (CHL, USACE) and Aggelos Dimakopoulos (HRW)
Background
When solving large-scale water-wave models, it is important to consider the fluid behaviour at the domain boundaries. For example, it's unrealistic for a coastal wave to interact with an invisible wall located a finite distance out to sea. We would expect the wave to travel off to the horizon unimpeded, instead of being reflected back towards the shore. In lieu of extending the model domain substantially in order to outrun such reflections, wave absorption techniques can be employed at reduced computational costs. When implemented at the so-called 'outflow' boundaries, these techniques effectively allow waves to exit the domain without producing significant unwanted backscatter.
There are two main types of absorption technique: passive, and active. Passive methods are those that do not vary in time with respect to outgoing waves. They typically involve introducing a sponge-like layer at the edge of the model domain, as illustrated below in Figure 1. As waves travel out of the original section of the domain and into this 'absorption layer', their amplitudes become damped. Ideally, the amplitudes are reduced smoothly to zero upon arrival at the extended 'far-field' boundary.
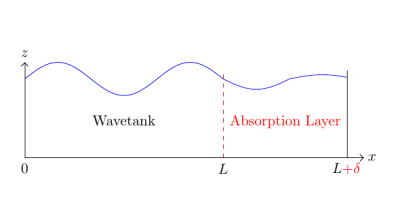
Figure 1: A 2D wavetank with a passive absorption layer.
Conversely, active methods are tailored to react according to the properties of outgoing waves. They generally take the form of an 'absorbing boundary condition', and replace any existing condition on the outflow boundary; this is shown in Figure 2. As waves approach the boundary, in satisfying this condition exactly they are transmitted out of the domain without causing spurious reflections.
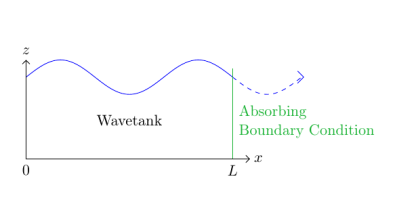
Figure 2: A 2D wavetank with an active absorbing boundary condition.
In this project, we aim to develop a more efficient wave absorption technique for use in Proteus, a Python-based computational methods and simulation toolkit.
Progress
Thus far, we have reviewed the current wave absorption technique utilised in Proteus. By simplifying our wavetank model to a 2D linear shallow-water scenario, and employing asymptotic analysis, we have determined some weaker aspects of the technique that have allowed for optimisation. Further, we have identified and resolved two unsatisfied criteria that were responsible for discontinuities in the fluid-velocity solution. Together, these improvements have reduced the magnitude of unwanted backscatter generated at the outflow boundary, and provided tailored bounds for the absorption layer width.
In addition to this, we have evaluated other existing absorption methods, and benchmarked their efficacy. In doing so, we have formulated a clear idea of the strengths and limitations typical of these techniques, and surmised the issues that need addressing going forward.
Future Work
Whilst we have a short-term solution for simple 2D linear shallow-water waves, we would like to extend our application further. In the next stage of the project, we will look to incorporate 3D, non-shallow water, and non-linear waves. In 3D in particular, we will encounter the non-trivial problem of wave directionality, where our current methods quickly fail for wide-angled 'glancing' waves. Additionally, we would like to explore the feasibility of combining a passive and an active absorption method to create a hybrid technique.
We may also consider the case of absorption in physical wavetanks, where large areas of sponge material are costly and inconvenient. Here, wave paddles are favoured to both generate and absorb water waves, however, accurate monitoring of the outgoing waves, and optimised control theory techniques are crucial in order to achieve effective real-time paddle motion.

