Mathematical Models of Particle Filtration
- Researcher: Arkady Wey
- Academic Supervisors: Chris Breward, Jon Chapman, Ian Griffiths
- Industrial Supervisor: Uwe Beuscher, Vasu Venkateshwaran
Background
Filtration is the process of removing particles from a fluid by passing it through a porous membrane. It is used across a huge range of industrial sectors, often for impurity removal and refinement. Research to improve the performance of filters is becoming increasingly important as we begin to understand the damage that harmful particles are doing to the planet.
W. L. Gore & Associates, Inc. (Gore) is a US-based company that offers medical and fabric solutions, and supplies filter membranes to a diverse set of end users. During filtration, a fluid containing a suspension of particles is driven through these membranes, usually by either a constant pressure-drop or constant flow-rate.
The particles are sometimes captured in the pores within the membrane. As a result, the particle concentration in the fluid passing out of the membrane is lower than that in the fluid passing in. The particles that the filter retains build up until the filter becomes clogged. This occurs when the permeability, which is the fluid conductivity of the filter, falls below an application-dependent critical value.
In the constant pressure-drop regime, this corresponds to the Darcy velocity, which is the volume of fluid that passes into the filter per unit time per unit area, falling below a critical value. In the constant flow-rate regime, this corresponds to the pressure-drop exceeding some critical value. When a filter is clogged, the filtration process must be halted while the filter is cleaned or sometimes replaced. This is expensive and time-consuming, and so clogging is undesirable. Our aim is to derive models of filtration that provide simple, fast, and non-destructive ways of understanding how to increase the amount of fluid that can be processed before the filter is clogged.
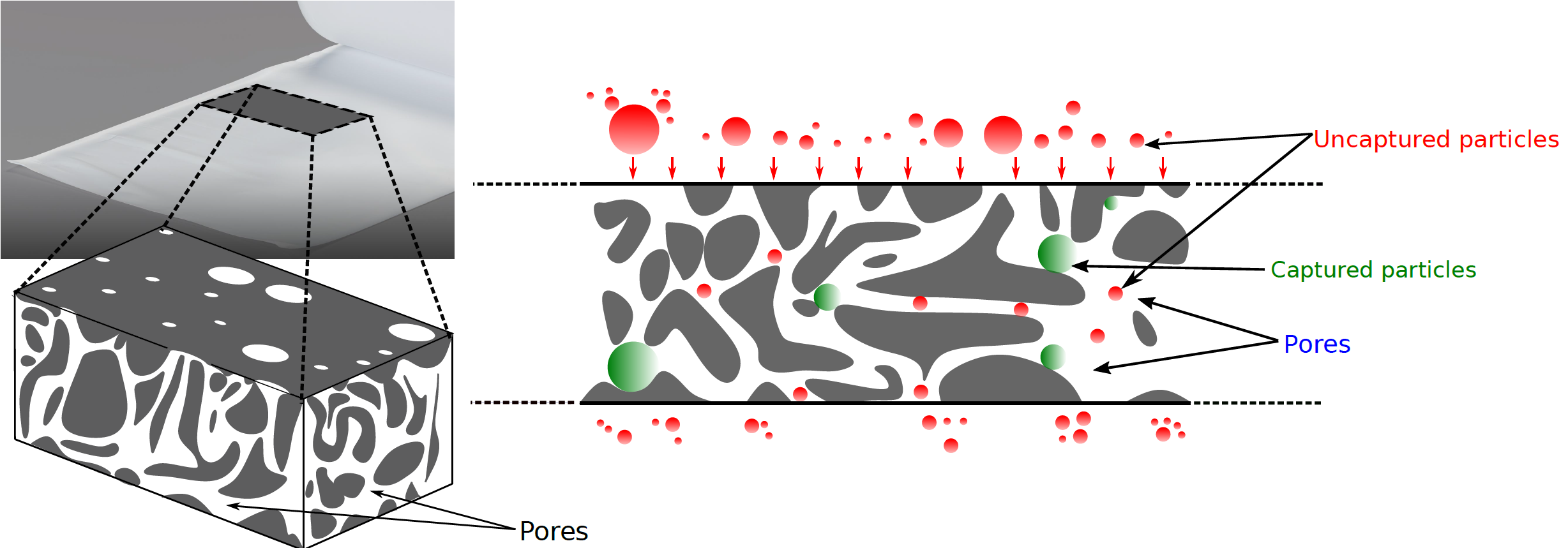
Figure 1: A photo of a membrane manufactured by Gore (available at www.gore.com) along with a diagram of a block of membrane in which pores are illustrated (left), and a diagram of the side-profile of a membrane during filtration, to show uncaptured and captured particles, and pores (right).
Progress
We have developed a size-structured continuum model of particle filtration. This consists of a set of partial differential equations that describe the evolution of the particle- and pore-size distributions. Changes in these distributions are the result of blocking, which occurs when a particle is too large to fit through a pore, and deposition, which occurs when a particle sticks to the inner wall of a pore. Our model allows us to predict the number of uncaptured and captured particles and pores of any size at any depth in the filter, at any time. Using these predictions, we simulate the permeability, which allows us to forecast the Darcy velocity in the filter. We use these quantities to predict the onset of filter clogging. At present, we are collaborating with experimentalists at Gore, in order to test our results against empirical data.
Figure 2: Graphs to show the pore-size distribution $n$ as a function of pore size $r$ at various depths $z$ and times $t$. The size-distribution of pores changes at all depths as particles are captured in pores. Changes are fastest at the top of the filter, where there are the most particles to capture.
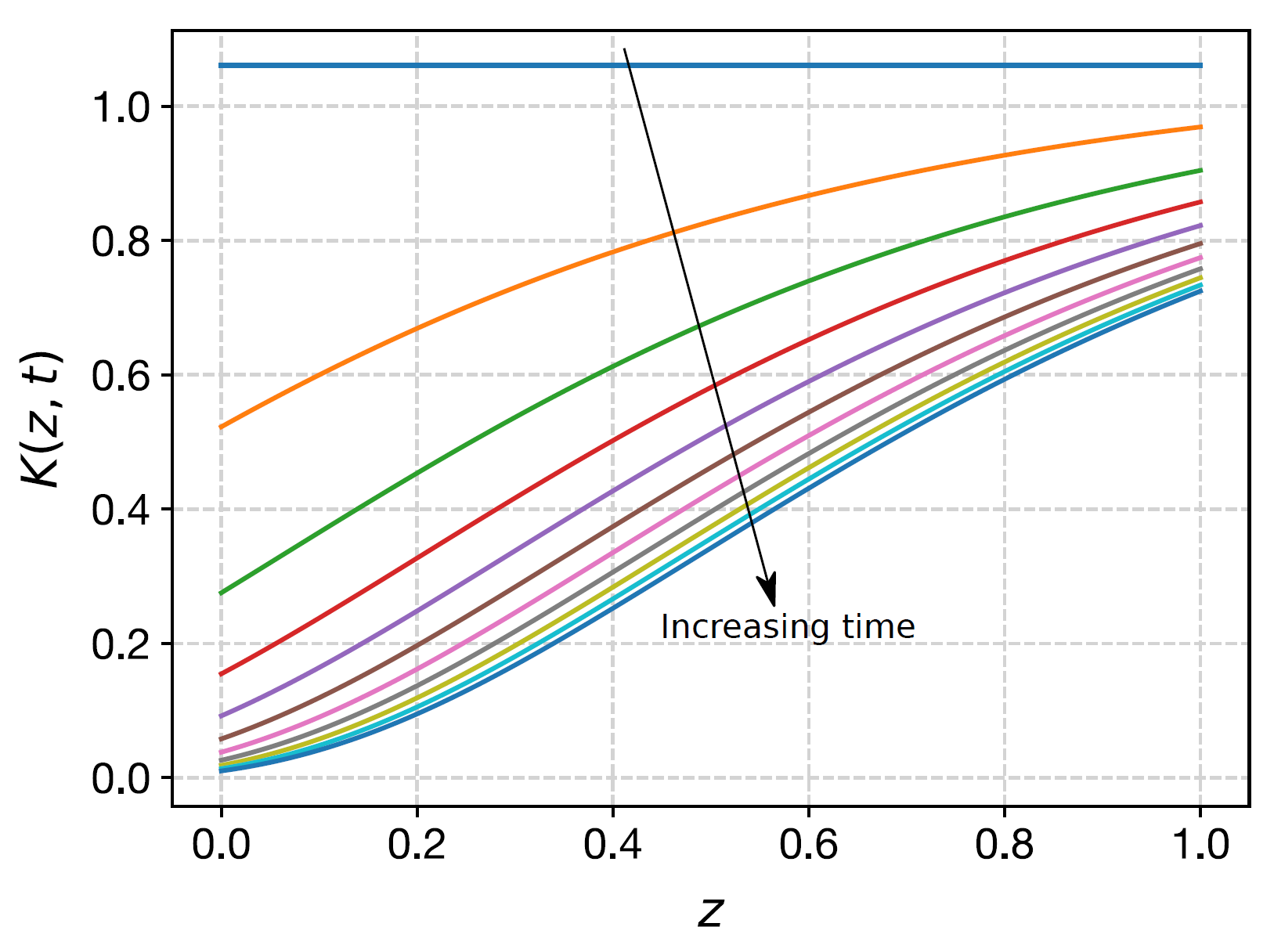
Figure 3: A graph to show the permeability $K$ as a function of depth $z$ at various times $t$. The permeability decreases in time at all depths as particles are captured in pores.
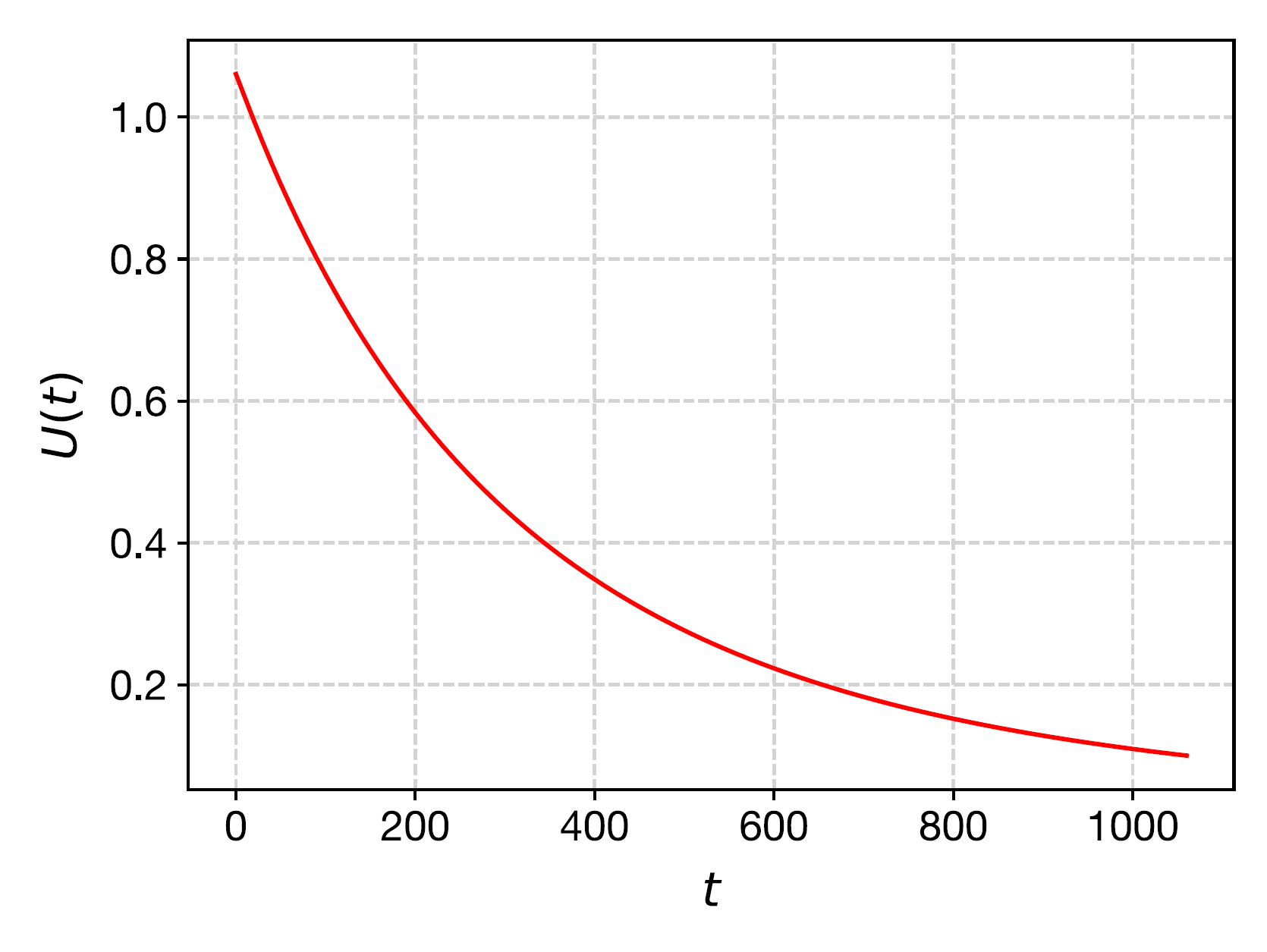
Figure 4: Graph to show the Darcy velocity $U$ as a function of time $t$. The Darcy velocity decreases as time increases, since the permeability decreases so that less fluid can travel through the filter per unit time.
Future Work
Next, we will develop a network model that describes fluid flow, particle capture, and pore removal on the microscale. We will tune this model to Gore's membranes by using experimental pore-connectivity data. We will then explore novel network homogenisation approaches, and use these to build a continuum description of filters on the macroscale that still preserves relevant pore-scale information. The resulting homogenised model should afford a significant computational improvement over both the discrete network model and our size-structured continuum model.