Predictive models of culture media stoichiometry for organoid expansion
- Researcher: Meredith Ellis
- Academic Supervisors: Sarah Waters, Helen Byrne, Mohit Dalwadi
- Industrial Supervisors: Marianne Ellis, Kim Luetchford, William Newell
Background
Organoids are three-dimensional multi-cellular structures, grown in vitro to recreate a realistic in vivo micro-anatomy. Organoids retain many features of the human tissues from which they are originally derived, such as the tissue structure, pathology, and heterogeneous cellular composition, making them a more representative proxy for in vivo cells than flat 2D cell line cultures.
The culturing of organoids is a highly labour intensive and time-consuming process, with small quantities and variability between batches. However, the development of suitable culture conditions has allowed Cellesce to utilise bioreactor technology to grow organoids at scale, making the process suitable for large-throughput drug screens. A key priority is ensuring reproducibility of organoid output and uniformity of organoid size, which depends on the bioreactor design and operating conditions.
In this project, we will develop a mechanistic mathematical model that will give quantitative predictions for the fluid flow profiles and the oxygen and metabolite concentrations, throughout the bioreactor. We seek to understand the effects of the operating parameters on organoid output. The model will then be used to optimise the bioreactor operating conditions that ensure the organoids are subject to appropriate fluid mechanical and concentration fields throughout the duration of culture.
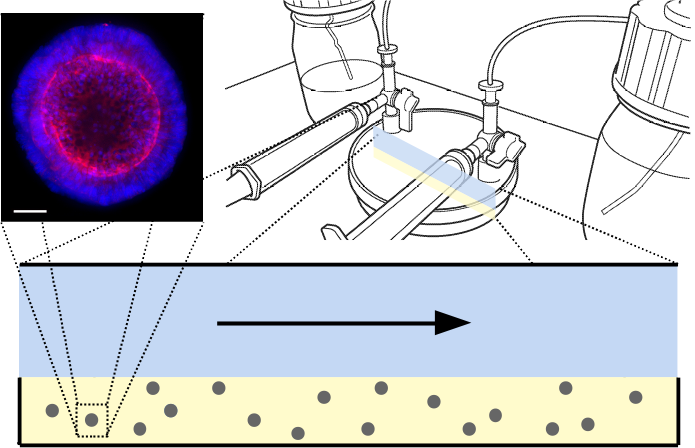
Figure 1: (Top left) Example of colorectal organoid*, stained for nuclear (blue) and cytoskeletal (red) markers for imaging. Scale 50µm. (Top right) Schematic of ‘CXP1’ bioreactor [1]. (Bottom) Two-dimensional reduction of bioreactor, with arrow showing direction of media flow. Blue is media, yellow is hydrogel, grey is organoid biomass.
*Courtesy of Mairian Thomas, Cellesce Ltd.
Progress
We have developed a dynamic two-dimensional continuum model for nutrient and waste metabolite transport within the CXP1 bioreactor [2]. We focus on the transport of glucose and lactic acid as our nutrient and waste metabolite, respectively, as current experimental data from Cellesce suggests these are the key limiting chemicals for organoid growth. Our model considers two distinct regions within the bioreactor – the effective hydrogel region, in which organoid behaviour is taken into account via effective reaction terms, and the liquid culture media, which flows across the hydrogel layer and is thought to facilitate nutrient provision to and waste removal from the organoids.
We used an asymptotic analysis to systematically derive two reduced models which exploit the extreme spatial and temporal parameter ratios in the system. Our model predicts the spatiotemporal distribution of the metabolic environment within the bioreactor - information which is challenging to obtain experimentally. Both reduced models are one-dimensional in space; the longwave approximation comprises two coupled reaction-advection-diffusion equations, whereas the sublimit approximation comprises two coupled reaction-advection equations. Our systematic analysis allows us to relate parameters in the reduced models to geometric and operating parameters of the CXP1 system, such as the ratio between the depth of the hydrogel and media layers, and the fluid flux over the hydrogel. We found that both reduced models provide good approximations of the full model for most physically relevant parameter regimes. Using the sublimit model, we obtain analytical solutions for the metabolite concentrations in the case of exponential cell growth.
We exploit our reduced mathematical models to determine the evolution of the spatial metabolite distributions throughout the bioreactor for a given inlet flow rate and cell seeding density. To assess the bioreactor transport characteristics, we introduce metrics quantifying glucose conversion (the ratio between the total amounts of consumed and supplied glucose), the maximum lactate concentration, the proportion of the bioreactor with intolerable lactate concentrations, and the time when intolerable lactate concentrations are first experienced within the bioreactor. These metrics are dependent both on bioreactor operating conditions and on organoid-line characteristics such as proliferation rate and rate of glucose consumption per cell. The relative importance of each metric will depend on the particular organoid line being investigated and the specific user requirements. Insights from this work can be used to inform desirable bioreactor operating conditions, ultimately improving the quality and number of bioreactor-expanded organoids.
Future Work
Future modelling work will consider individual organoids as small regions within the hydrogel where local glucose consumption and lactate production occur, and the organoid growth will depend on these concentrations. We will use a mathematical homogenisation approach (see [3, 4]) to systematically average the behaviour over the microscale to obtain a macroscale governing equation for the hydrogel layer with effective glucose consumption, lactate production, and organoid growth terms.
This in turn will give us an understanding of the relationship between the bioreactor operating parameters and the mean and variation in organoid size, ultimately facilitating optimisation of the bioreactor operating conditions to minimise organoid size variation.
References
[1] Ellis, M. J., Chaudhuri, J., and Dale, T. C. (2019). Methods for culturing organoids. U.S. Patent Application No. 16/316,573. Washington, DC: U.S. Patent and Trademark Office
[2] Ellis, M. A., Dalwadi, M. P., Ellis, M. J., Byrne, H. M., and Waters, S.L. (2021) A systematically reduced mathematical model for organoid expansion. Frontiers in Bioengineering and Biotechnology (forthcoming)
[3] Dalwadi, M. P., Wang, Y., King, J. R., and Minton, N. P. (2018). Upscaling diffusion through first-order volumetric sinks: A homogenization of bacterial nutrient uptake. SIAM Journal on Applied Mathematics 78, 1300–1329. doi:10.1137/17M1138625
[4] Dalwadi, M. P. and King, J. R. (2020). A systematic upscaling of nonlinear chemical uptake within a biofilm. SIAM Journal on Applied Mathematics 80, 1723–1750. doi:10.1137/19M130220X


