Solutions - 2021
Part of the Oxford MAT Livestream
These are the solutions for the Logarithms and powers worksheet.
Here's a copy of what was written on-screen during the livestream
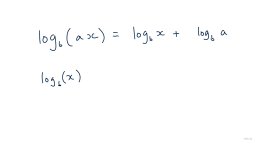 |
 |
 |
 |
Warm-up
- Simplify $\log_{10} 3+\log_{10} 4$ into a single term.
- This is $\log_{10} 12$.
- If we write $a=\ln 2$ and $b=\ln 5$, then write the following in terms of $a$ and $b$. \[\ln 1024, \quad \ln 40, \quad \ln \sqrt{2/5}, \quad \ln 1/10, \quad \ln 1.024.\]
- $\ln 1024=\ln\left(2^{10}\right)=10\ln 2=10a$.
- $\ln 40=\ln 8+\ln 5=3a+b$.
- $\ln \sqrt{2/5}=\frac{1}{2}\ln 2/5=\frac{1}{2}\left(a-b\right)$.
- $\ln 1/10=-\ln 10=-\ln2-\ln 5=-a-b$.
- $\ln 1.024=\ln 1024+\ln 1/1000=10a +3(-a-b)=7a-3b$.
- There are other solutions, partly because $b=a\times\log_2 5$.
- Expand $\left(e^x+e^{-x}\right)\left(e^y-e^{-y}\right)+\left(e^x-e^{-x}\right)\left(e^y+e^{-y}\right)$.
- $e^{x+y}+e^{y-x}-e^{x-y}-e^{-x-y}+e^{x+y}-e^{y-x}+e^{x-y}-e^{-x-y}$.
- That's $2e^{x+y}-2e^{-x-y}$.
- Expand $\left(e^x+e^{-x}\right)\left(e^y+e^{-y}\right)+\left(e^x-e^{-x}\right)\left(e^y-e^{-y}\right)$.
- $e^{x+y}+e^{y-x}+e^{x-y}+e^{-x-y}+e^{x+y}-e^{y-x}-e^{x-y}+e^{-x-y}$.
- That's $2e^{x+y}+2e^{-x-y}$.
- Solve $2^x=3$. Solve $0.5^x=3$. Solve $4^x=3$.
- $2^x=3$ is what it means for $x$ to be $\log_2 3$.
- If $0.5^x=3$ then $2^{-x}=3$ so $x=-\log_2 3$. Alternatively, just write down $x=\log_{0.5}3$.
- If $4^x=3$ then $2^{2x}=3$ so $x=\frac{1}{2}\log_2 3$. Alternatively, just write down $x=\log_4 3$.
- For which values of $x$ (if any) does $1^x=1$? For which values of $x$ (if any) does $1^x=3$?
- $1^x=1$ is true for all real $x$.
- $1^x$ is never equal to 3 for real $x$.
MAT questions
MAT 2015 Q1H
- That's a very strange logarithm. The only way I can think of to get rid of it is to write \[4-5x^2-6x^3=(x^2+2)^2.\]
- Now this is a polynomial question (but we should be careful to go back and check our solutions in the original equation).
- The polynomial rearranges to $x^4+6x^3+9x^2=0$.
- Either $x=0$ or $x^2+6x+9=0$ which has a repeated root $x=-3$.
- Let's quickly check these solutions $\log_2(4)=2$ and $\log_{11}(4-45+162)=\log_{11}121=2$.
- There are two distinct solutions.
- The answer is (c).
MAT 2017 Q1I
- Let's simplify each term. $\log_b\left(\left(b^x\right)^x\right)=x\log_b \left(b^x\right)=x^2\log_b b =x^2$.
- Also, $\log_a\left(\frac{c^x}{b^x}\right)=x\log_a(c/b)=x\left(\log_a c-\log_a b\right)$.
- And the last term is $-\log_a b\log_a c$.
- So this is a quadratic. Even better, we can factorise it \[x^2+\left(\log_a c-\log_a b\right)x-\log_a b\log_a c=\left(x-\log_a b\right)\left(x+\log_a c\right).\]
- Those roots are the same number if $\log_a b=-\log a_c$, which happens when $c=1/b$.
- The answer is (d).
MAT 2013 Q1F
- The only way that we can have $\log_b a=2$ is if $a=b^2$. Similarly, we must have $c-3=b^3$ and $c+5=a^2$.
- These simultaneous equations aren't linear, but we can do our best to solve them.
- For example, we must have $c+5=b^4$ and $c-3=b^3$, so $b^4-b^3=8$. How many solutions does that have?
- Let's sketch $b^3(b-1)$ for $b>0$ (since we're told that $b$ is positive).
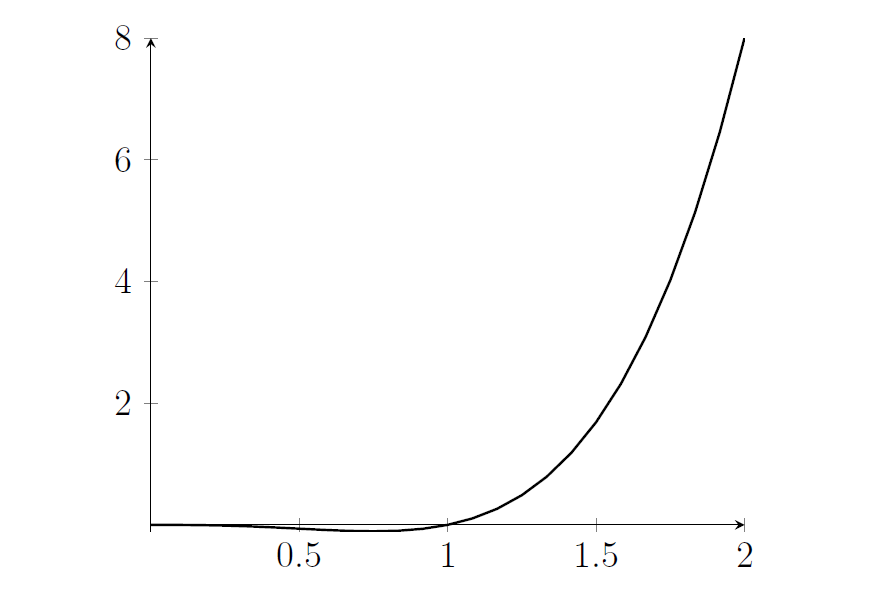
- This is negative in between $0$ and $1$ and then after that it's positive and increases (because $(b-1)$ and $b^3$ are both increasing functions). It can only have one solution for $b^3(b-1)=8$. In fact, that solution is $b=2$, but what we're interested in for this question is that that's a unique solution.
- Now look back at the other equations. We've got $a=b^2=4$ and $c=3+b^3=11$. Let's check the original logarithms. \[ \log_2 4=2,\qquad \log_2 (11-3)=3,\qquad \log_4 (11+5)=2\]
- These equations specify $a$ uniquely (it's 4).
- The answer is (a).
MAT 2013 Q1J
- This is some new notation. It appears in the question in the expression $[2^x]$, which mean the largest integer less than or equal to $2^x$.
- When $x=0$, the term $[2^x]$ is 1. It stays at 1 until we get to a point with $2^x=2$, because then the largest integer less than or equal to $2^x$ will be 2 instead. That happens when $x=1$. Then $2^x$ keeps increasing, but the largest integer under it is still 2, until we get to a point with $2^x=3$.
- Time for a logarithm; that happens when $x=\log_2 3$. There's a pattern here; the function takes each value between 1 and $2^{n-1}$ (it doesn't quite get to $2^n$ until right at the end of the interval when $x=n$).
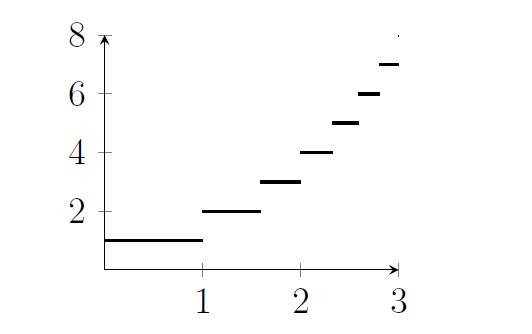
- When we integrate this function from 0 to $n$, we're calculating the area under the graph. That's made of a series of rectangles, and the sum of the areas of those rectangles is \[ 1+(\log_2 3-1)\times 2+ (\log_2 4-\log_2 3)\times 3 +(\log_2 5-\log_2 4)\times 4+\dots + (n-\log_2(2^n-1))\times \left(2^n-1\right) \]
- There's a pattern here (add some $\log_2 k$ then subtract slightly more $\log_2 k$) and it simplifies to \[ -1-\log_2 3-\log_2 4-\dots -\log_2 (2^n-1)+n(2^n-1)\]
- That's $-\log_2\left(\left(2^n-1\right)!\right)+n\left(2^n-1\right)$ which is not quite one of the options.
- But $\log_2 2^n=n$ so we can re-write this as $-\log_2 \left(\left(2^n\right)!\right)+n2^n$.
- The answer is (b).
Reflection
- I really like logarithms, but in lots of these questions getting rid of the logarithm is a good thing to do!
- In that last question, we simplified things by using laws of logarithms and also by using the $k!$ notation for $k\times(k-1)\times\dots\times 2\times1$, which is a very compact way to write that product.

