Configuration spaces of particles and phase transitions
Abstract
Configuration spaces of points in Euclidean space or on a manifold are well studied in algebraic topology. But what if the points have some positive thickness? This is a natural setting from the point of view of physics, since this the energy landscape of a hard-spheres system. Such systems are observed experimentally to go through phase transitions, but little is known mathematically.
In this talk, I will focus on two special cases where we have started to learn some things about the homology: (1) hard disks in an infinite strip, and (2) hard squares in a square or rectangle. We will discuss some theorems and conjectures, and also some computational results. We suggest definitions for "homological solid, liquid, and gas" regimes based on what we have learned so far.
This is joint work with Hannah Alpert, Ulrich Bauer, Robert MacPherson, and Kelly Spendlove.
Hilbert schemes of points of ADE surface singularities
Abstract
I will discuss some recent results around Hilbert schemes of points on singular surfaces, obtained in joint work with Craw, Gammelgaard and Gyenge, and their connection to combinatorics (of coloured partitions) and representation theory (of affine Lie algebras and related algebras such as their W-algebra).
On Serre's Uniformity Conjecture
Abstract
Given a prime p and an elliptic curve E (say over Q), one can associate a "mod p Galois representation" of the absolute Galois group of Q by considering the natural action on p-torsion points of E.
In 1972, Serre showed that if the endomorphism ring of E is "minimal", then there exists a prime P(E) such that for all p>P(E), the mod p Galois representation is surjective. This raised an immediate question (now known as Serre's uniformity conjecture) on whether P(E) can be bounded as E ranges over elliptic curves over Q with minimal endomorphism rings.
I'll sketch a proof of this result, the current status of the conjecture, and (time permitting) some extensions of this result (e.g. to abelian varieties with appropriately analogous endomorphism rings).
12:45
Supersymmetric phases of N = 4 SYM at large N
Abstract
We show the existence of an infinite family of complex saddle-points at large N, for the matrix model of the superconformal index of SU(N) N = 4 super Yang-Mills theory on S3 × S1 with one chemical potential τ. The saddle-point configurations are labelled by points (m,n) on the lattice Λτ = Z τ + Z with gcd(m, n) = 1. The eigenvalues at a given saddle are uniformly distributed along a string winding (m, n) times along the (A, B) cycles of the torus C/Λτ . The action of the matrix model extended to the torus is closely related to the Bloch-Wigner elliptic dilogarithm, and its values at (m,n) saddles are determined by Fourier averages of the latter along directions of the torus. The actions of (0,1) and (1,0) agree with that of pure AdS5 and the Gutowski-Reall AdS5 black hole, respectively. The actions of the other saddles take a surprisingly simple form. Generically, they carry non vanishing entropy. The Gutowski-Reall black hole saddle dominates the canonical ensemble when τ is close to the origin, and other saddles dominate when τ approaches rational points.
From neurons to random matrices and dynamics
Abstract
This talk will be a survey on the applications of random matrix theory in neuroscience. We will explain why and how we use random matrices to model networks of neurons in the brain. We are mainly interested in the study of neuronal dynamics, and we will present results that cover two parallel directions taken by the field of theoretical neuroscience. First, we will talk about the critical point of transitioning to chaos in cases of random matrices that aim to be more "biologically plausible". And secondly, we will see how a deterministic and a random matrix (corresponding to learned structure and noise in a neuronal network) can interact in a dynamical system.
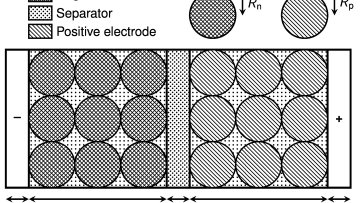
Have you ever wished that the battery on your phone would last longer? That you could charge it up more rapidly? Maybe you have thought about buying an electric vehicle, but were filled with range anxiety – the overwhelming fear that the battery will run out before you reach your destination, leaving you stranded? Oxford Mathematicians are hard at work demonstrating that mathematics may provide the key to help tackle problems faced by the battery industry.
What is Arakelov Geometry?
Abstract
Arakelov geometry studies schemes X over ℤ, together with the Hermitian complex geometry of X(ℂ).
Most notably, it has been used to give a proof of Mordell's conjecture (Faltings's Theorem) by Paul Vojta; curves of genus greater than 1 have at most finitely many rational points.
In this talk, we'll introduce some of the ideas behind Arakelov theory, and show how many results in Arakelov theory are analogous—with additional structure—to classic results such as intersection theory and Riemann Roch.
Cartier Operators
Abstract
Given a morphism of schemes of characteristic p, we can construct a morphism from the exterior algebra of Kahler differentials to the cohomology of De Rham complex, which is an isomorphism when the original morphism is smooth.