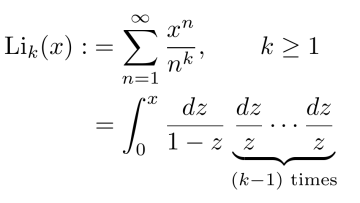The goal of the talk is to present a proof of the following statement:
Let (K,v) be an algebraic extension of (Q_p,v_p) whose completion is perfectoid. We show that K is relatively decidable to its tilt K^♭, i.e. if K^♭ is decidable in the language of valued fields, then so is K. 
In the first part [of the talk], I will try to cover the necessary background needed from model theory and the theory of perfectoid fields.

We study a class of non linear integro-differential equations on the Wasserstein space related to the optimal control of McKean-Vlasov jump-diffusions. We develop an intrinsic notion of viscosity solutions that does not rely on the lifting to an Hilbert space and prove a comparison theorem for these solutions. We also show that the value function is the unique viscosity solution. Based on a joint work with V. Ignazio, M. Reppen and H. M. Soner

In the seminar I will present a recent work joint with  S. Suhr (Bochum) giving an optimal transport formulation of the full Einstein equations of general relativity, linking the (Ricci) curvature of a space-time with the cosmological constant and the energy-momentum tensor. Such an optimal transport formulation is in terms of convexity/concavity properties of the Shannon-Bolzmann entropy along curves of probability measures extremizing suitable optimal transport costs. The result gives a new connection between general relativity and  optimal transport; moreover it gives a mathematical reinforcement of the strong link between general relativity and thermodynamics/information theory that emerged in the physics literature of the last years.

I will give an overview of the localization technique: a powerful dimension-reduction tool for proving geometric and functional inequalities.  Having its roots in a  pioneering work of Payne-Weinberger in the 60ies about sharp Poincare’-Wirtinger inequality on Convex Bodies in Rn, recently such a technique found new applications for a range of sharp geometric and functional inequalities in spaces with Ricci curvature bounded below.

It is known that many real-world networks exhibit geometric properties.  Brain networks, social networks, and wireless communication networks are a few examples.  Storage and transmission of the information contained in the topologies and structures of these networks are important tasks, which, given their scale, is often nontrivial.  Although some (but not much) work has been done to characterize and develop compression limits and algorithms for nonspatial graphs, little is known for the spatial case.  In this talk, we will discuss an information theoretic formalism for studying compression limits for a fairly broad class of random geometric graphs.  We will then discuss entropy bounds for these graphs and, time permitting, local (pairwise) connection rules that yield maximum entropy properties in the induced graph distribution.