The chameleon's tongue is said to unravel at the sort of speed that would see a car go from 0-60 mph in one hundredth of a second – and it can extend up to 2.5 body lengths when catching insects. Oxford Mathematicans Derek Moulton and Alain Goriely have built a mathematical model to explain its secrets.
On groups with quadratic Dehn functions
Abstract
I am going to discuss Rips' conjecture that all finitely presented groups with quadratic Dehn functions have decidable conjugacy problem.
This is a joint work with A.Yu. Olshanskii.
Cutpoints of CAT(0) groups
Abstract
It is known that if the boundary of a 1-ended
hyperbolic group G has a local cut point then G splits over a 2-ended group. We prove a similar theorem for CAT(0)
groups, namely that if a finite set of points separates the boundary of a 1-ended CAT(0) group G
then G splits over a 2-ended group. Along the way we prove two results of independent interest: we show that continua separated
by finite sets of points admit a tree-like decomposition and we show a splitting theorem for nesting actions on R-trees.
This is joint work with Eric Swenson.
Finiteness Properties and Free Abelian Subgroups
Abstract
Finiteness properties of groups come in many flavours, I will discuss topological finiteness properties. These relate to the finiteness of skelata in a classifying space. Groups with interesting finiteness properties have been found in many ways, however all such examples contains free abelian subgroups of high rank. I will discuss some constructions of groups discussing the various ways we can reduce the rank of a free abelian subgroup.
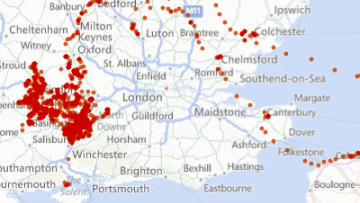
The use of mathematical models to describe the motion of a variety of biological organisms has been the subject of much research interest for several decades. If we are able to predict the future locations of bacteria, cells or animals, and then we subsequently observe differences between the predictions and the experiments, we would have grounds to suggest that the local environment has changed, either on a chemical or protein scale, or on a larger scale, e.g.
T-duality and the condensed matter bulk-boundary correspondence
Abstract
This talk will start with a brief historical review of the classification of solids by their symmetries, and the more recent K-theoretic periodic table of Kitaev. It will then consider some mathematical questions this raises, in particular about the behaviour of electrons on the boundary of materials and in the bulk. Two rather different models will be described, which turn out to be related by T-duality. Relevant ideas from noncommutative geometry will be explained where needed.
17:00
How Can We Understand Our Complex Economy? - Doyne Farmer
Abstract
We are increasingly better at predicting things about our environment. Modern weather forecasts are a lot better than they used to be, and our ability to predict climate change illustrates our better understanding of our effect on our environment. But what about predicting our collective effect on ourselves? We now use tools like Google maps to predict how long it will take us to drive to work, and other small things, but we fail miserably when it comes to many of the big things. For example, the recent financial crisis cost the world tens of trillions of pounds, yet our ability to forecast, understand and mitigate the next economic crisis is very low. Is this inherently impossible? Or perhaps we are just not going about it the right way? The complex systems approach to economics, which brings in insights from the physical and natural sciences, presents an alternative to standard methods. Doyne will explain what this new approach is and give a few examples of its successes so far. He will then present a vision of the economics of the future which will need to confront the serious problems that the world will soon face.
Please email @email to register
Appearing everywhere from state-of-the-art cryptosystems to the proof of Fermat's Last Theorem, elliptic curves play an important role in modern society and are the subject of much research in number theory today. Jennifer Balakrishnan, a researcher working in number theory, explains more in the latest in our Oxford Mathematics Alphabet.
Introduction to Beilinson's approach to p-adic Hodge theory
Abstract
This is an introduction to the article
A. Beilinson, p-adic periods and derived de Rham cohomology, J. Amer. Math. Soc. 25 (2012), no. 3, 715--738.