Second Order Optimisation for Machine Learning

• Researcher: Constantin Octavian Puiu
• Academic Supervisor: Coralia Cartis
• Industrial Supervisor: Jan Fiala

Background

Optimisation problems form the modelling and numerical core of machine learning and statistical methodologies, such as in the training of supervised machine learning classifiers. In such applications, a large amount of data (feature vectors) is available that has been already classified (namely labelled). Then a parameterised classifier is selected and trained on this data, namely, values of the parameters are calculated so that the output of the classifier at the given features matches their labels in some optimal way. The ensuing classifier is then used for testing, in order to label/classify unseen data. The training problem is formulated as an optimisation problem that minimises, for example, the average amount of errors that the classifier makes on the test set. Various formulations of the optimisation problem are used, most commonly considering some continuous loss function to measure the error at each data point and either (deterministic) finite sum or (probabilistic) expectation of the loss terms as the total error; the latter may be convex (such as in the case of binary classification) but, more and more nowadays, it may instead be nonconvex due to the prevalence of deep learning applications. The scale of the ensuing optimisation is commonly huge, with millions of parameters and terms in the objective sum of functions. This makes the calculation of a single function or gradient value prohibitively expensive and leads to the need for inexact optimisation algorithms that effectively exploit problem structure. The practical method of choice in ML applications is the (batch) stochastic gradient method (Robbins-Munro, 1950) that computes only the gradients of a small, randomly chosen number of the loss terms and controls both variance and convergence by means of a predefined step size. A grand challenge in this area is how to augment stochastic gradient methods with inexact second order derivative information, so as to obtain more efficient methods especially in the nonconvex case of deep learning, both in terms of achieving higher accuracy but also robustness to ill-conditioning.

In this project, we investigate ways to approximate second-order information in the finite-sum structure of ML optimisation problems, from subsampling second-order derivatives to approximating them by differences in batch gradients, such as in block (stochastic) quasi-Newton approaches and Gauss-Newton methods. In place of the usual predefined step size, we will consider the impact of more sophisticated step size techniques from classical optimisation that are adaptive to local optimisation landscapes such as variable/adaptive trust-region radius, regularisation and line search. We will also consider preconditioning techniques that contain inexpensive second-order derivative information. We will also investigate parallel and decentralised implementations of these methods, which is a challenge especially for higher-order techniques.

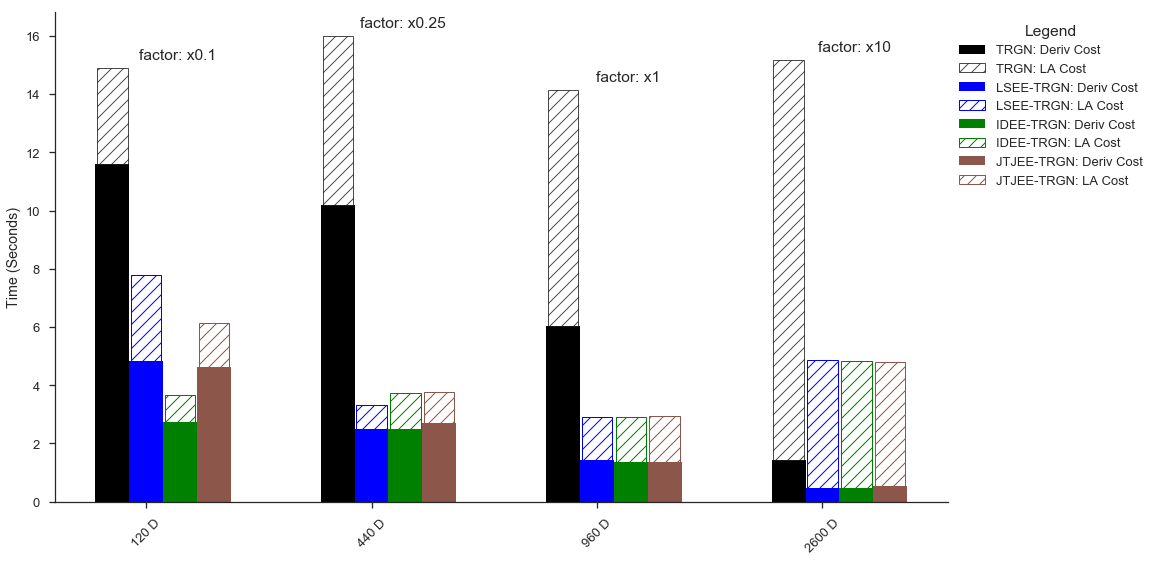
Figure 1: Example improvement for the proposed algorithm, for different parameter space sizes (e.g. 120 parameters)

Outcomes

We started from the simplest problem: classical optimisation. We developed a framework to speed up derivative-based optimisation algorithms when the derivatives are not analytically available. We do so by periodically taking subspace steps in a well chosen subspace. The figure shows the amount of speedup we can hope for when using our proposed approach. The next step is trying to combine this idea with Natural gradient methods, which seem to be the most successful second order optimisation methods for ML.