Oxford Mathematician Andras Juhasz discusses and illustrates his latest research into knot theory.
Schauder theory for uniformly degenerate elliptic equations
Abstract
The uniformly degenerate elliptic equation is a special class of degenerate elliptic equations. It appears frequently in many important geometric problems. For example, the Beltrami-Laplace operator on conformally compact manifolds is uniformly degenerate elliptic, and the minimal surface equation in the hyperbolic space is also uniformly degenerate elliptic. In this talk, we discuss the global regularity for this class of equations in the classical Holder spaces. We also discuss some applications.
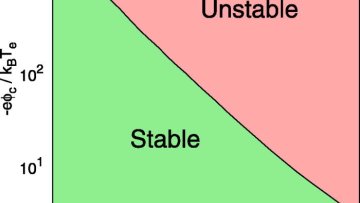
Oxford Mathematician John Allen, Professor Emeritus of Engineering Science, talks about his work on the electrohydrodynamic stability of a plasma-liquid interface. His collaborators are Joshua Holgate and Michael Coppins at Imperial College.
Oxford Mathematician John Ball has won the European Academy of Sciences Leonardo da Vinci award. The award is given annually for outstanding lifetime scientific achievement. In the words of the Committee, "through a research career spanning more than 45 years, Professor Ball has made groundbreaking and highly significant contributions to the mathematical theory of elasticity, the calculus of variations, and the mathematical analysis of infinite-dimensional dynamical systems."
The Usefulness of a Modified Restricted Isometry Property
Abstract
The restricted isometry property is arguably the most prominent tool in the theory of compressive sensing. In its classical version, it features l_2 norms as inner and outer norms. The modified version considered in this talk features the l_1 norm as the inner norm, while the outer norm depends a priori on the distribution of the random entries populating the measurement matrix. The modified version holds for a wider class of random matrices and still accounts for the success of sparse recovery via basis pursuit and via iterative hard thresholding. In the special case of Gaussian matrices, the outer norm actually reduces to an l_2 norm. This fact allows one to retrieve results from the theory of one-bit compressive sensing in a very simple way. Extensions to one-bit matrix recovery are then straightforward.
15:30
Joint NT/LO Seminar: Rational points and ultrproducts
Abstract
There is a conjecture by Colliot-Thelene (about 2005) that under specific hypotheses, a morphism of Q-varieties f : X --> Y has the property that for almost all prime numbers p, the corresponding map X(Q_p) --> Y(Q_p) is surjective. A sharpening of the conjecture was solved by Denef (2016), and later, "if and only if" conditions on f were given by Skorobogatov et al. The plan for the talk is to explain in detail the conjecture and the results mentioned above, and to report on work in progress on a different method to attack the conjecture under quite relaxed hypotheses.