Oxford Mathematician Konstantin Ardakov has been awarded the 2020 Adams Prize. The Adams Prize is awarded jointly each year by the Faculty of Mathematics, University of Cambridge and St John’s College, Cambridge to UK-based researchers, under the age of 40, doing first class international research in the Mathematical Sciences.
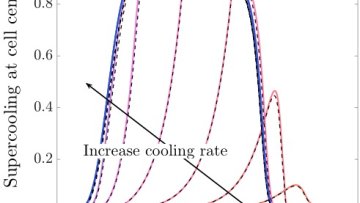
Oxford Mathematician Mohit Dalwadi talks about his work on the modelling of cryopreservation.
The University has announced numerous steps to prioritise the health and welfare of staff, students and visitors in the light of the UK’s escalating coronavirus situation. This is an unprecedented and challenging time for our university and department community, and I would ask that you please support each other wherever you can, and follow University guidance, which is continuously updated. MI staff and students should also check their emails regularly for further guidance.
Oxford Mathematicians Derek Moulton and Alain Goriely together with their colleague Régis Chirat (University of Lyon) have won the 2019 PNAS Cozzarelli Prize in the Engineering and Applied Sciences category for their paper 'Mechanics unlocks the morphogenetic puzzle of interlocking bivalved shells.'
Multi-Objective Resource Allocation for Cognitive Radio Networks (An Exercise in Study Group Management)
Abstract
In this talk we will discuss a problem that was worked on during MISGSA 2020, a Study Group held in January at The University of Zululand, South Africa.
We look at a communication network with two types of users - Primary users (PU) and Secondary users (SU) - such that we reduce the network to a set of overlapping sub-graphs consisting of SUs indexed by a specific PU. Within any given sub-graph, the PU may be communicating at a certain fixed frequency F. The respective SUs also wish to communicate at the same frequency F, but not at the expense of interfering with the PU signal. Therefore if the PU is active then the SUs will not communicate.
In an attempt to increase information throughput in the network, we instead allow the SUs to communicate at a different frequency G, which may or may not interfere with a different sub-graph PU in the network, leading to a multi-objective optimisation problem.
We will discuss not only the problem formulation and possible approaches for solving it, but also the pitfalls that can be easily fallen into during study groups.
15:00
Decomposition of 2d theories with 1-form symmetries
Abstract
In this talk, we will discuss two-dimensional theories with discrete
one-form symmetries, examples (which we have been studying
since 2005), their properties, and gauging of the one-form symmetry.
Their most important property is that such theories decompose into a
disjoint union of theories, recently deemed `universes.'
This decomposition has the effect of restricting allowed nonperturbative
sectors, in a fashion one might deem a `multiverse interference effect,'
which has had applications in topics including Gromov-Witten theory and
gauged linear sigma model phases. After reviewing one-form symmetries
and decomposition in general, we will discuss a particular
example in detail to explicitly illustrate these properties and
to demonstrate how
gauging the one-form symmetry projects onto summands in the
decomposition. If time permits, we will briefly review
analogous phenomena in four-dimensional theories with three-form symmetries,
as recently studied by Tanizaki and Unsal.
12:45
Bottom-up construction of 4d N=2 SCFTs
Abstract
In this talk, I will argue how the observation that four-dimensional N=2 superconformal field theories are interconnected via the operation of Higgsing can be turned into an effective method to construct such SCFTs. A fundamental role is played by the (generalized) free field realization of the associated VOAs.
Connections in symplectic topology
Abstract
Here, a connection is a algebraic structure that is weaker than an algebra and stronger than a module. I will define this structure and give examples. I will then define the quantum product and explain how connections capture important properties of this product. I will finish by stating a new result which describes how this extends to equivariant Floer cohomology. No knowledge of symplectic topology will be assumed in this talk.