Source Reconstruction from Hydrophone Data

• Researcher: Bogdan Toader
• Academic Supervisors: Jared Tanner and Andrew Thompson
• Industrial Supervisors: Peter Harris and Stephane Chretien

Background

Given a number of moving point sources emitting sound in a specific region, we want to estimate the overall sound and the exact locations and paths of the sources by taking only a small number of measurements of the sound in the region. We model the problem using the framework of superresolution, where the (unknown) input signal is a discrete measure (sum of Diracs) and the measurements consist of samples of the convolution of the signal with a known kernel, for example a Gaussian. In Figure 1 we show an example of such a signal in one dimension; the aim is to recover the discrete signal (blue spikes) from the noisy measurements (black circles). These techniques represent an equivalent of compressed sensing in a continuous setting.

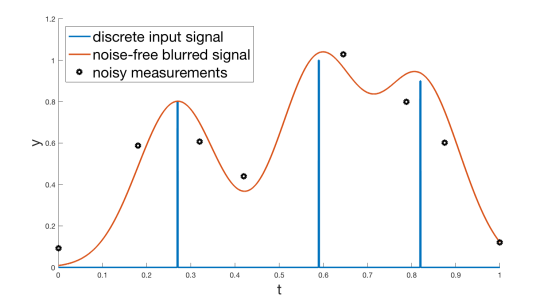
Figure 1. Example of discrete input signal and noisy samples.

The goal of this project was to develop theory and algorithms for solving the deconvolution problem. Firstly, we want to know under what conditions it is possible to find the correct solution, or an approximation to it, since the measurements are noisy in a real-world scenario. These conditions are related to the number of measurements, their locations relative to the locations of the point sources and the width of the convolution kernel. Secondly, once it is established that the problem can be solved, we want to develop a method for provably recovering the locations and intensities of the point sources.

Outcomes

The project consisted of two parts, one for each objective listed above: a stability analysis to show that, under the appropriate conditions, it is possible to recover an approximation to the true signal from noisy measurements, and a perturbation analysis of the relationship between the primal and the dual problem, motivated by applying a non-smooth optimisation algorithm to the deconvolution problem.

Stability Analysis

In most of the literature in this area, the focus is on solving the total variation norm minimisation problem, where we seek a 'sparse' non-negative measure which matches the observed measurements. This is a continuous analog of the 1-norm minimisation problem for vectors, common in compressed sensing. However, in our work we have considered the feasibility problem for nonnegative measures; that is, we seek any measure which matches the observed measurements. This is motivated by the existing literature in compressed sensing, where it has been shown that under the non-negativity assumption, the true signal is the unique signal consistent with the measurements.

By relying on the machinery of the Chebyshev systems, we have shown that the true signal is the only solution of the feasibility problem in the noise-free, one-dimensional case. In the more difficult case when the measurements are corrupted by additive noise, we want to control the magnitude of the error between the true signal and the solution to the feasibility problem on intervals around each source and away from the sources. In [1,2], we have shown that if, for each source, there exist two nearby samples, the error depends linearly on the level of noise. This result is stated both for a general convolution kernel/point spread function, and more explicitly for the case when the convolution kernel is Gaussian, when the constants in the error bounds are explicit. This is the first result of this kind in the setting of noisy measurements and positive measures where the focus is on the feasibility problem and not on a particular relaxation or method of solving the problem. This Company logo implies that our error bounds hold regardless of the algorithm used for solving the super-resolution problem.

Perturbation Analysis

The second outcome of this project is a perturbation analysis of the relationship between the primal problem and the dual problem, which is relevant for solving the problem in practice. One way of approaching the deconvolution problem is by applying a non-smooth convex optimisation algorithm, for example the level method, to the exact penalty formulation of the dual problem. While this is a well known method in the convex optimisation literature, it is a new approach in the context of superresolution. From the solution to the dual problem, given by the convex optimisation algorithm, we then obtain the locations of the points sources by finding the global maximisers of the dual certificate formed by the dual solution, and the intensities of the point sources by solving a least squares problem. The question then is, given inaccuracies in the dual solution due to noise or numerical errors, how large the error in the source locations and intensities is. We consider such inaccuracies in the dual variable to be perturbations of its true solution in a ball of small radius. In [3], we apply a quantitative version of the implicit function theorem in a novel manner to show how the size of the perturbation in the dual variable around its true value bounds the perturbations in the point source locations and intensities around their true values. These are practically error bounds in the solution when the super-resolution problem is solved using its dual, as a function of the error of the dual solution, which can expressed further as a function of the measurement noise.

Publications

[1] Eftekhari A., Tanner, J., Thompson, A., Toader, B., & Tyagi, H. (2018, June). Non-negative Super-resolution is Stable. Proceedings of 2018 IEEE Data Science Workshop (DSW).
[2] Eftekhari, A., Tanner, J., Thompson, A., Toader, B., & Tyagi, H. (2019). Sparse non-negative super-resolution—simplified and stabilised. Applied and Computational Harmonic Analysis.
[3] Chretien, S., Thompson, A., & Toader, B. (2019). The dual approach to non-negative super-resolution: impact on primal reconstruction accuracy. In Proceedings of 2019 13th International conference on Sampling Theory and Applications (SampTA).