Silicon Anodes in Lithium-Ion Batteries
 Researcher: Ian Roper
Researcher: Ian Roper- Academic Supervisors: Jon Chapman and Colin Please
- Industrial Supervisor: Bill Macklin
Background
Lithium-ion batteries are used in almost all portable electronic devices, including laptops and mobile phones. More recently, research into these batteries has increased due to the emergence of the electronic vehicle market. Lithium-ion batteries function by lithium atoms stored in the anode splitting into a Li+ ion and an electron. The Li+ ion moves through the electrolyte to the cathode whereas the electron travels around an external circuit, inducing a current and generating power. This is shown in the Figure 1. At the cathode surface, the electron and the Li+ ion recombine to a lithium atom which intercalates into the cathode. When the battery is charged, the opposite process occurs and the lithium is intercalated back into the anode.
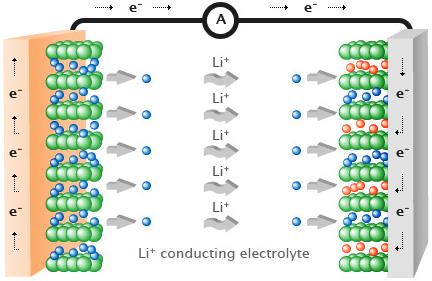
Figure 1: Schematic of a lithium-ion battery.
One of the challenges facing the lithium-ion battery sector is increasing the amount of energy that can be used from a single charge of the battery, which is known as the capacity of the anode. The capacity is determined by the amount of lithium that can be stored in the anode and is typically measured with respect to the volume or the mass of the anode.
One anode material with an especially large capacity for lithium is silicon, much larger than the commonly-used graphite. However, when fully lithiated, silicon anodes expand to around four times their original size, compared to graphite expanding to only 1.1 times its original size. This expansion can displace other components of the battery and induce large stresses in the anode material, causing it to crack. This can lead to loss of connectivity, causing the capacity of the battery to fade over time. The stresses in the anode are induced in two ways: i) by other components of the battery constraining the expanding anode and ii) by a non-uniform distribution of lithium within the anode causing different parts of the anode to expand by different amounts.
Several experimental attempts to mitigate the effects of the expansion of silicon have been carried out by designing nano-structures. This is so that the diffusion length of the lithium into the anode is smaller, meaning the distribution of lithium within the anode is more uniform, mitigating the stresses caused by the non-uniformity of lithium. Examples of these nano-structures include nano-particles, nano-wires and nano-tubes. A second method for mitigating the expansion of the silicon is to use a different anode material to constrain the silicon’s expansion. This has led to designs such as core–shell, yolk–shell and coated nano-wires.
In my project, I focus on a core–shell anode nano-particle design with a silicon core and a graphite shell. I concentrate on the very slow charging case such that we may ignore the diffusion of lithium through the anode nano-particle. Instead, for a given amount of lithium, known as the state of charge (SOC), we calculate the displacement and stresses induced by the presence of multiple anode materials as well as the lithium concentration throughout the nano-particle. The overall aim of the project is to find core–shell nano-particle designs which mitigate the expansion of the silicon without sacrificing the high capacity of the silicon core.
Outcomes
The slow-charging assumption implies that the chemical potential of the lithium throughout the anode nano-particle is uniform. A phenomenon known as stress-assisted diffusion is incorporated into the model, so that the mechanical stress affects the lithium concentration as well as the lithium concentration inducing the mechanical stress. Therefore, the chemical potential consists of a stress-independent part based on the open-circuit voltage (OCV) of the anode material, and a stress-dependent part proportional to the hydrostatic stress in the anode material.
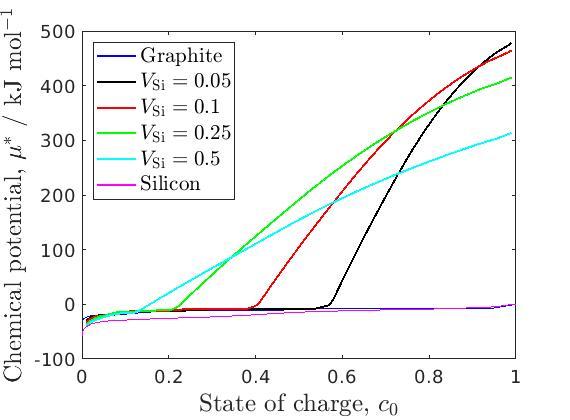
Figure 2: Effective OCV.
Even with the stress-coupling, we find that the lithium concentration is uniform across each anode material when charging slowly. Additionally, as the chemical potential of each material must be the same, we are able to find an ‘effective’ OCV of the multi-material anode nano-particle. Measuring OCVs experimentally is both time-consuming and expensive, so approximating the OCV of multi-material anode designs using this model is very beneficial. These effective OCVs are shown in the figure. Scott – same thing. Lastly, we are able to show that stress-assisted diffusion has a very large effect on the lithium distribution between the silicon and the graphite.
The stress and displacement throughout the nano-particle are calculated for a given initial volume of silicon core and a given SOC. Using these results, different measures used to optimise the size of the silicon core in the core–shell nano-particle are proposed based on the capacity of the nano-particle, the expanded volume, and the maximum stress resulted in different optimal designs. For example, the optimal design to maximise the capacity under an expanded volume constraint is a nano-particle which has an expanded volume equal to the constraint when fully lithiated.
Porous silicon is incorporated to improve on these optimal designs of the simple core–shell nano-particle. The material properties of the porous silicon are estimated using a homogenisation method known as the method of multiple scales. Using these effective material properties, we incorporate the porous silicon into the nano-particle in two ways: i) in place of the non-porous silicon core and ii) as a porous layer between the non-porous silicon core and the graphite shell. We find that when fully charged, the use of porous silicon can mitigate the expansion of the nano-particle without sacrificing the capacity of the nano-particle.
Using linear elasticity to describe the mechanics of the materials cannot capture all of the phenomena that occur in lithium-ion anodes during lithiation. For example, linear elasticity relies on the assumption that the displacements are small, which is not the case for the expansion of silicon at high lithium concentrations. We also analyse a geometrically nonlinear elasticity model to describe the anode materials, and find that this model cannot be solved for high states of charge or large silicon core volumes. However, if the constitutive law of the materials (which determines how the elastic energy in the material varies with the mechanical strain) is also considered to be nonlinear, solutions can be found for all states of charge.
Finally, if the stress in the materials become too high, the graphite and the silicon will mechanically yield by either cracking or flowing plastically. For core–shell nano-particles, this is a large concern if the graphite shell is yielded at its outer radius. We use a simple model to approximate the relationship between the size of the silicon core and the SOC at which the entire graphite shell yields. This simple model can also be used to approximate the size and distribution of small silicon particles scattered in a large matrix of graphite, a design which Nexeon is currently manufacturing.

