Modelling the Influence of Ureteroscopes on Urological Flows and Stone Dynamics
 Researcher: Jessica Williams
Researcher: Jessica Williams- Academic Supervisors: Sarah Waters, Derek Moulton and Ben Turney
- Industrial Supervisors: Tim Harrah, Niraj Rauniyar and Robert Lund
Background
A common, minimally invasive procedure for the removal of kidney stones is flexible uretero-renoscopy. This involves inserting a hand-held medical instrument, a flexible ureteroscope, to the location of the stone via the urethra, which provides passage through the bladder to the upper urinary system (Figure 1). Auxiliary working tools are placed through the working channel to fragment and remove stones.
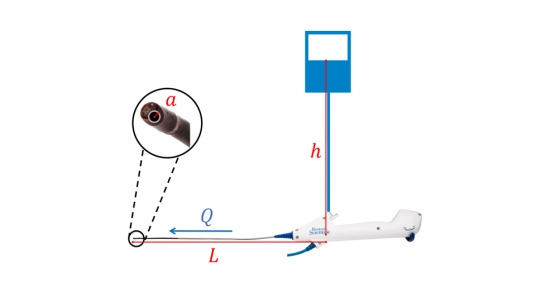
Figure 1: A ureteroscope inserted into the kidney with access sheath for outflow.
One of the primary challenges of ureteroscopic procedures is visualisation within the kidney environment as this requires irrigation with a physiologic saline solution, both to clear the field of view of debris, and to open up the ureter and renal cavities to provide access for the scope. This irrigation is typically achieved by hanging a saline bag above the scope to provide a continuous flow through the ureteroscope and into the kidney, with a return flow through an access sheath. However, the details of the flow, specifically its impact on intrarenal pressure and the clearance of debris, are hard to determine.
This is where mathematical modelling has significant potential value, as a physics based model can provide intuition for fundamental system behaviour. We model the flow of irrigation fluid through the ureteroscope, access sheath, and within the renal pelvis by considering systematic reductions of the Navier-Stokes equations and using a combination of analytical, numerical, and experimental techniques to rigorously address questions of design and optimality.
Outcomes
We derived mathematical models to describe the irrigation flow through a ureteroscope in various configurations, motivated by pipe flow theory, and tested the validity of these models with laboratory experiments, demonstrating good agreement [1]. Results determined that auxiliary working tools provide a large resistance to flow that is highly dependent upon the cross-sectional geometries of the working channel and working tool. We determined an optimal elliptical shape for the working channel containing a working tool – equivalently the access sheath containing the scope shaft – that maximises flow rate for a fixed pressure drop [2, Figure 2].
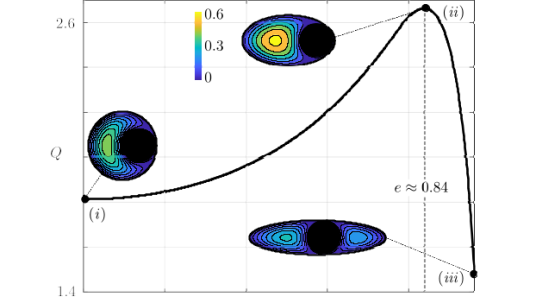
Figure 2: A plot of flow rate as a function of elliptical eccentricity of the working channel (fixing cross-sectional area). At each eccentricity, the tool is positioned at the location within the channel that maximises flow.
We combined models for flow through the working channel and access sheath with an exponential constitutive law for kidney compliance to derive a systems model for ureteroscopy irrigation; an ordinary differential equation for kidney pressure with an associated algebraic expression for flow rate. This simple model demonstrated excellent agreement with the results of ex-vivo experiments [3].
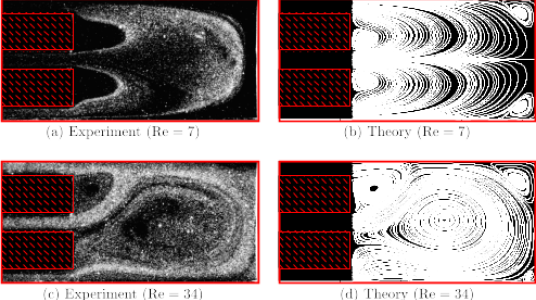
Figure 3: Theoretical and experimental comparison of flow in the simplified geometry representing the renal pelvis. The Reynolds number (Re) captures the relationship between viscous and inertial forces and is set by the flow rate.
We also studied flow within a simplified geometry representing the renal pelvis and characterised the existence of multiple solutions to the steady, Navier-Stokes equations in the considered domain. We demonstrated excellent agreement with particle image velocimetry experiments, conducted in collaboration with A.A. Castrejon-Pita (Figure 3). We performed simulations to determine the diffusion and advection of a passive tracer by the computed velocity fields, representing the movement of kidney stone dust within the renal pelvis. We classified the dependence of the time required to clear the renal pelvis of the passive tracer on the Peclet number, which characterises the relative contributions of advection and diffusion.
Publications
[1] J. G. Williams, B. W. Turney, N. P. Rauniyar, T. P. Harrah, S. L. Waters and D. E. Moulton, The Fluid Mechanics of Ureteroscope Irrigation, Journal of Endourology, 2019.
[2] J. G. Williams, B. W. Turney, D. E. Moulton and S. L. Waters, The effect of geometry on resistance in elliptical coaxial pipe flows, Journal of Fluid Mechanics, 2019 (Submitted).
[3] J. G. Williams, L. Rouse, B. W. Turney, S. L. Waters and D. E. Moulton, A lumped parameter model for kidney pressure during stone removal, IMA Journal of Applied Mathematics, 2019 (Submitted).

