Electrochemical Modelling of Batteries for Off-Grid Energy Storage Systems

- Researcher: Valentin Sulzer
- Academic Supervisors: Jon Chapman, David Howey, Charles Monroe and Colin Please
- Industrial Supervisor: Chris Baker-Brian
Background
As renewable energy sources become cheaper and more efficient, they are used increasingly to take over from fossil fuels in producing electricity. Since these sources are inherently fluctuating, the supply must be smoothed out by energy storage, in particular using batteries. Lead-acid batteries are a cheap, safe, reliable and recyclable solution for off-grid energy storage, and thus are used by BBOXX, who design, manufacture and distribute solar home systems to improve energy access in the developing world.

Figure 1. BBOX Battery.
In our work, we develop reduced-order models of lead-acid batteries, which have the high accuracy of complex models but low computational cost of simple models. These can then be used to track and manage the batteries, with the aim of improving their discharge and charge efficiency, and increasing their lifetime.
Outcomes
We started by modelling the batteries as one-dimensional, with the dimension of interest being across the electrodes and separator. By considering the movement of electrically charged ions in the electrolyte, the reactions occurring in the porous electrodes, and the distribution of current across the system, we developed a homogenised system of Differential-Algebraic Equations (DAEs), known as a “porous-electrode model”.
Using non-dimensionalisation, we identified key parameters in the model that control the response of the battery. The most important of these is the diffusional C-rate (the ratio between the diffusion timescale and discharge timescale), which is low at most practical current values. By performing a perturbation expansion in this small parameter, we obtained a series of reduced-order models of increasing complexity and accuracy. The simplest, leading-order model gave an algebraic expression for the voltage, and was found to be accurate up to C-rates of 0.1C. Quasi-static corrections to the leading-order model were given by the first-order model, which has the same complexity but gives increased accuracy up to 1C. A further more complex, composite, model required solving an additional linear PDE, and was found to be accurate up to 5C.
In addition to accurate voltage predictions for less computational complexity, the reduced-order models gave physical insight into the problem by allowing us to more easily decompose the voltage into its constituent parts. Further, we demonstrated that reduced-order models can allow accurate parameter fitting with reduced computational cost (an example of such a fit is shown in Figure 2).
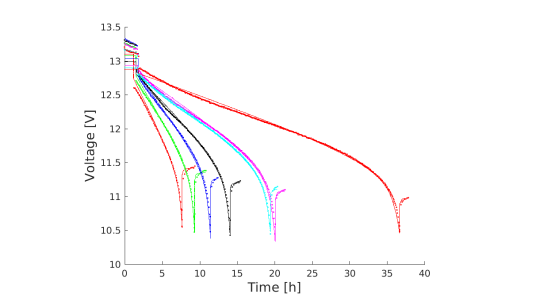
Figure 2: Model fit to BBOXX data. Circles are data and lines are model; different colours represent different discharges at different currents (0.5A - 3A).
Second, we considered three-dimensional models of lead-acid batteries, and used the fact that the aspect ratio of the batteries is small to decompose the transverse direction from the planar directions. We found good agreement between our decomposed model and the solution of the full three-dimensional model, obtained using COMSOL. Our model showed that more current crosses the separator near the top of the battery than near the bottom, and so the battery discharges more quickly at the top.
We then explored three further asymptotic limits as we varied the electrode conductivity and diffusional C-rate, each providing a different trade-off between accuracy and speed. By comparing of all the different limits as we varied electrode conductivity and C-rate, we were able to suggest which model was most appropriate in each parameter regime.
Finally, we extended our model to specifically include oxygen evolution and recombination during recharge. The resulting model displayed the known behaviour that oxygen recombination in the negative electrode must be diffusion-limited. Hence we adapted the standard equations for oxygen kinetics and transport to model the diffusion-limited system. We showed that the reduced-order modelling framework developed for discharge could easily be extended to the case of recharge with an additional reaction, and the reduced-order models agreed well with the full-order model in the appropriate parameter regimes. Further physical insight was provided by the reduced-order models as they showed that the non-monotonicity of the voltage increase that was observed during charge must be due to diffusion-limited effects.
All of the results in this thesis (both full- and reduced-order), as well as similar results for lithium-ion batteries, were implemented in the open-source Python package “PyBaMM” (Python Battery Mathematical Modelling), which was developed as part of this work in collaboration with other battery researchers.
Publications
[1] Sulzer, V., Chapman, S. J., Please, C. P., Howey, D. A., & Monroe, C. W. (2019). Faster Lead-Acid Battery Simulations from Porous-Electrode Theory: Part I. Physical Model. Journal of The Electrochemical Society, 166(12), A2363-A2371.
[2] Sulzer, V., Chapman, S. J., Please, C. P., Howey, D. A., & Monroe, C. W. (2019). Faster Lead-Acid Battery Simulations from Porous-Electrode Theory: Part II. Asymptotic Analysis. Journal of The Electrochemical Society, 166(12), A2372-A2382.
[3] Marquis, S. G., Sulzer, V., Timms, R., Please, C. P., & Chapman, S. J. (2019). An asymptotic derivation of a single particle model with electrolyte. Journal of The Electrochemical Society, 166(15), A3693-A3706
[4] Sulzer, V., Marquis, S. G., Timms, R., Robinson, M., & Chapman, S. J. (2019). PyBaMM: Python Battery Mathematical Modelling. Submitted to Journal of Open Research Software.

