Characterising the Behaviour of Bifurcating Systems with Parameter Distribution
 Researcher: Ana Osojnik
Researcher: Ana Osojnik- Academic Supervisors: Helen Byrne, Eamonn Gaffney
- Industrial Supervisors: James Yates, Michael Davies
Background
Cancer can invade and spread to different parts of the body from where it started, which makes this disease difficult to be controlled by standard treatments of care such as chemotherapy, radiotherapy or invasive surgery. A new promising tool is immunotherapy, which aims to stimulate the body's immune system to attack cancer cells.
Figure 1: Tumour cell under immune attack.
Despite the success of immunotherapy treatments, data from trials as in Figure 2 often show a separation of tumour responses into two groups; uncontrolled tumour growth, and tumour shrinkage (or eradication). Such observations may be caused by heterogeneity of the tumour population and the tumour microenvironments. This suggests that a better understanding of interactions between tumour and immune cells is needed to improve immunotherapeutic treatments and increase response rates. Mechanisms of tumour-immune interactions are complex, and so mathematical modelling can be used as a tool to gain further insight.
In a mathematical model that describes tumour-immune interactions, tumour heterogeneity can be thought of as a distribution of model parameters over a tumour population. In view of that, our aim is to investigate whether a mechanistic model, which exhibits bifurcating switches or bistability between different tumour growth regimes can explain the observed separation of tumour responses to treatment. For example, if the model’s resting states correspond to different stages of immunoediting (escape, equilibrium, eradication), then changes in behaviour as parameters or initial conditions are varied can represent the transitions between tumour escape and eradication that are seen in the data.
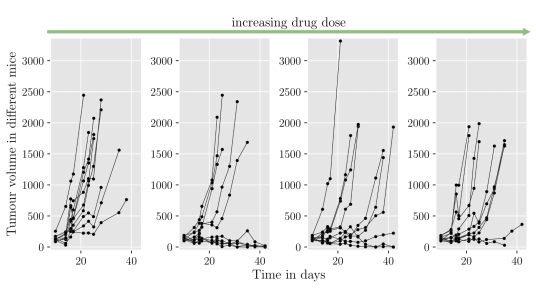
Figure 2: Tumour volume data against time from mouse studies where a type of an immunotherapeutic drug was administered.
Progress
The challenge with validation of mathematical models of tumour-immune interactions is finding a balance between model complexity and feasibility of estimating model parameters from (often scarce and sparse) experimental data. In light of this, we have considered a minimally parametrised, mechanistic model from the literature that describes interactions between tumour and immune cells in a fixed tumour region. We have shown that the quasi-steady state approximation (QSSA) used in literature is not an appropriate model simplification, as the behaviour and the bifurcation structure of the QSSA are inconsistent with the full model. Using matched asymptotics, we have derived a valid simplified model. Through systematic variation of the model parameters we have shown that the model demonstrates tumour escape, dormancy, and eradication, as well as bistability between tumour escape and dormancy, as desired (see Figure 3). Interestingly, we have shown that the model exhibits excitable behaviour in the considered parameter region. For example, we see large excursions in the phase space as well as emergence of limit cycles with switching spikes in the number of tumour or immune cells.
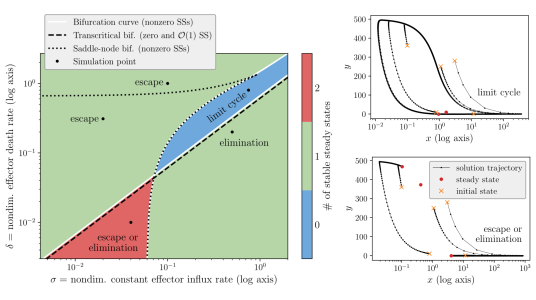
Figure 3: Attracting resting states in parameter space (left) and phase portraits (right) with trajectories simulated using parameter values at simulation points marked in the left plot.
Future Work
In future, we will explore the feasibility of estimating parameters of the model analysed so far and similar bifurcating models, given tumour growth curves from preclinical immunotherapy drug studies shown above. Moreover, we would like to incorporate immunotherapy and stochastic effects into the model, and investigate it from the parameter estimation viewpoint.

