Optimisation of time parallelisation for applications in fusion plasma physics

• Researcher: Giancarlo Antonucci
• Academic Supervisor(s): Raphael Hauser
• Industrial Supervisor(s): Debasmita Samaddar

Background

For decades, researchers have been studying efficient numerical methods to solve differential equations, most of them optimised for one-core processors. However, in the context of the research conducted at the Culham Centre for Fusion Energy (CCFE), the highly nonlinear nature of the physics involved often leads to very long wall-clock times for the simulations of interest, usually beyond the reach of existing supercomputers. Therefore, CCFE are looking to modern parallel architectures to reduce the number of computations required by those extremely intensive simulations.

In this context, parallelisation across space typically reaches saturation at around a few thousand processors. When this happens, parallelisation across time is a promising way to provide more parallelism. The goal of this project is to formulate time-parallel optimisation techniques specific to chaotic dynamical systems for applications in fusion plasma physics. Such optimisation algorithms should make better use of parallel resources, yielding a high computational gain, and allow us to explore a variety of cases relevant to CCFE.

Progress

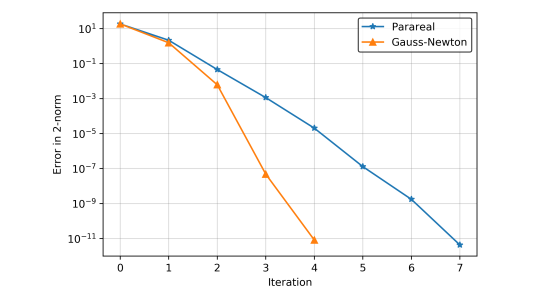
The Parareal algorithm has received much attention in the last two decades, mainly due to its simplicity and applicability; it has been successfully applied to various complex plasma physics simulations. Starting from Parareal, we have designed new time-parallel algorithms based on standard convex optimisation. The techniques we have developed have improved convergence in theory and practice, as shown in Figure 2. This can be explained by the fact that these methods perform further work to give more sensible corrections to the iterates. This does not decrease the overall scalability of the algorithms, as we can execute the extra computations in parallel.

Future Work

We are currently working towards applying the techniques we have developed to more complex chaotic models, which are representative of the type of plasma physics problems typically encountered by CCFE. Based upon these results, we will then refine our techniques for this class of problems.