Research Topics

The interests of the research group lie at the intersection between analysis and probability, with motivations coming from various other areas of science, ranging from physics to finance and data-science or biology. The need to consider models involving randomness at various scales or in high-dimensions have peculiar difficulties and opportunities which allow to develop mathematical theories beyond classical settings.

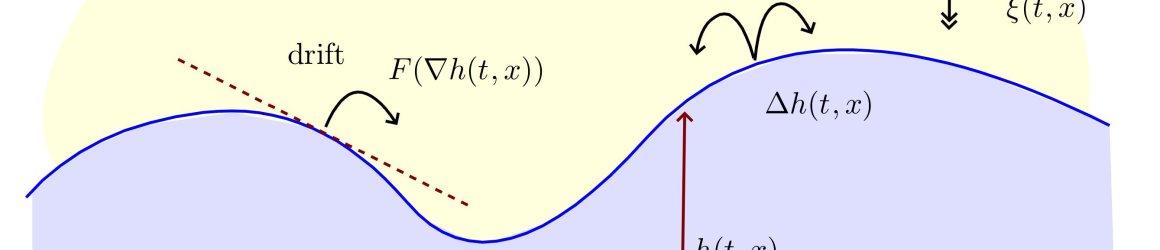
A good example of this synergy is the rough path theory, initiated by T. Lyons. At its core, it a pure mathematical theory motivated by the desire to extend the theory of differential equations to the situation where the terms are randomand too rough to use the usual PDE/ODE techniques. Many other members of the group made important contributions to the rough path theory (R. Cont, M. Gubinelli, B. Hambly, H. Oberhauser and Z. Qian).

Abstractly these developments involve the construction of analytical tools based on non-smooth reference objects which replace polynomials, including new notions of solutions to (partial) differential equations and new calculi suitable to handle generalised functions in non-linear context. Future work in this direction aims to extend these construction to include more complex geometrical settings like manifolds and fibre bundles, also motivated by construction of low dimensional Euclidean quantum gauge theories. By the intrinsic unifying nature of mathematics, the similar ideas are suited also to analyse situations in statistics where high-dimensional data have to be summarised efficiently for the use in machine learning, like in the research of H. Oberhauser.

The group is also quite active in direction of random matrix theory with J. Keating and L. P. Arguin.

D. Beliaev works on the geometry of random complex functions where interesting phenomena require notions of statistical mechanics, in particular percolation theory. Z. Qian studies random multiscale phenomena connected with fluid turbulence while B. Hambly and A. Etheridge work on discrete random models and their continuum limits, in particular with biological motivations.