Doctor of Philosophy (DPhil)
What is a DPhil?
A DPhil is Oxford's name for a PhD - a higher research degree which allows you to make an original contribution to mathematics in the form of a thesis. A DPhil takes three to four years to complete. During your DPhil, you will be supervised by at least one academic, although some students will have more than one supervisor (particularly if they are working across disciplines). Unlike CDT courses (and PhDs in other countries), you will begin to do research straight away and there is no prescribed taught component.
As part of your study toward a DPhil in Mathematics at Oxford, you will also be required to complete broadening and skills training and deliver class teaching to undergraduates, to enhance your broader mathematical knowledge and develop your career. You are very welcome to attend seminars and there may also be journal clubs or seminar series specific to your area of study.
If you enjoy doing mathematics, and would like to be part of a lively and world-class research institute, take a look at our research groups to see if they align with your own interests.
How to apply
All applications should be submitted online through the University's Graduate Application Form. Before you apply, check that you can meet the entry requirements, and read the University of Oxford's graduate application guide.
Key Deadlines
Application deadlines for the DPhil in Mathematics:
- 8th January 2026
- 3rd March 2026
Please apply by the 8th January deadline to be considered for available University-administered or Departmental scholarships.
Martingale Foundation Postgraduate Scholarships
The Martingale Foundation awards fully funded Scholarships for postgraduate degrees in the mathematical sciences at research universities in the UK.
Tuition fees and research expenses are fully covered, and Scholars receive a tax free living wage stipend. Martingale Scholars also receive access to leadership and career develop through a multi-year programme of training and support. Visit the Martingale website for more information.
Applications for the 2026 academic year are open until 24 October 2025.
Why do a PhD?
Fees, Funding and Scholarships
Full details about the applicable University fees and scholarships are available on the Fees and Funding webpage.
The University offers a wide range of scholarships, either administered centrally (available to all applicants to the University), or through the Department. All applicants that apply by the January application deadline and are made an offer of a place will be considered for Departmental and relevant University-administered scholarships. More details about the available scholarships and how they work is available on our Scholarships webpage and University's funding page.
Research Groups
Algebra
Research interests: group theory, representation theory and algebraic aspects of geometry.
Combinatorics
Research interests: extremal combinatorics, graph theory, and combinatorial number theory.
Functional Analysis
Research interests: operator theory, including unbounded operators, and abstract differential equations.
Geometry

Research interests: algebraic geometry, geometric representation theory, and differential geometry.
History of Mathematics

Research interests: history of algebra (19th and 20th century), history of modern algebra, and Soviet mathematics.
Logic
Research interests: analytic topology, geometric stability theory, and the model theory of p-adic fields and diophantine geometry.
Machine Learning and Data Science

Machine Learning and Data science are being developed using wide ranging mathematical techniques. Our particular research expertise include: applied and computational harmonic analysis, networks, optimisation, random matrix theory, rough paths, topological data analysis, and the application of these methods.
Mathematical & Computational Finance
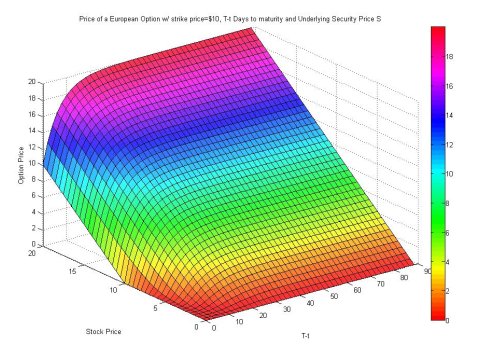
Research interests: behavioural finance, financial big data, high dimensional numerical methods, stochastic analysis.
Mathematical Biology

Research interests: cancer modelling, collective behaviour, gene regulatory networks, multiscale modelling, pattern formation, and sperm dynamics.
Mathematical Physics
Research interests: gauge and gravity theories (quantum field theories), string theory, twistor theory, Calabi-Yau manifolds, quantum computation and cryptography.
Number Theory
Research interests: analytic number theory, arithmetic geometry, prime number distribution, and Diophantine geometry.
Numerical Analysis

Research interests: complexity in optimisation, symmetric cone programming, numerical solutions of PDEs.
Oxford Centre for Industrial and Applied Mathematics
Research interests: energy, industry, geoscience, networks, finance, methodologies.
Oxford Centre for Nonlinear Partial Differential Equations

Research interests: geometric analysis, inverse problems, nonlinear hyperbolic systems, specific PDE systems.
Stochastic Analysis
Research interests: rough path theory, Schramm-Loewner evolution, mathematical population genetics, financial mathematics, self-interacting random processes.
Topology

Research interests: geometric group theory, 3-manifold topology and knot theory, K-theory, algebraic topology.


