Oxford Mathematician Karin Erdmann specializes in the areas of algebra known as representation theory (especially modular representation theory) and homological algebra (especially Hochschild cohomology). Here she discusses her latest work.
At the beginning of the twentieth century, some minor algebraic investigations grabbed the interest of a small group of American mathematicians. The problems they worked on had little impact at the time, but they may nevertheless have had a subtle effect on the way in which mathematics has been taught over the past century.
90% of the world’s data have been generated in the last five years. A small fraction of these data is collected with the aim of validating specific hypotheses. These studies are led by the development of mechanistic models focussed on the causality of input-output relationships. However, the vast majority of the data are aimed at supporting statistical or correlation studies that bypass the need for causality and focus exclusively on prediction.
At the beginning of the 20th century, Jacques Hadamard gave the definition of well-posed problems, with a view to classifying “correct” mathematical models of physical phenomena. Three criteria should be fulfilled: a solution exists, that solution is unique, and it should depend continuously on the parameters.
Oxford Mathematician Paul Moore talks about his application of mathematical tools to identify who will be affected with Alzheimer's.
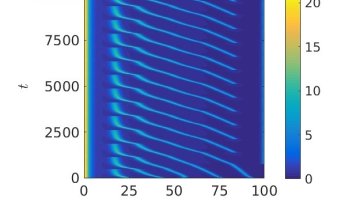
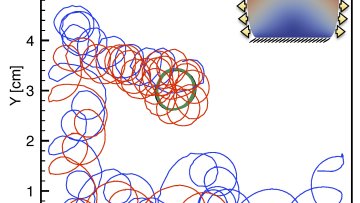
In a seminal 1952 paper, Alan Turing mathematically demonstrated that two reacting chemicals in a spatially uniform mixture could give rise to patterns due to molecular movement, or diffusion. This is a particularly striking result, as diffusion is considered to be a stabilizing mechanism, driving systems towards uniformity (think of a drop of dye spreading in water).
Everyday life tells us that curved objects may have two stable states: a contact lens (or the spherical cap obtained by cutting a tennis ball, see picture) can be turned ‘inside out’. Heuristically, this is because the act of turning the object inside out keeps the central line of the object the same length (the centreline does not stretch significantly). Such deformations are called ‘isometries’ and the ‘turning inside out’ (or everted) isometry of a thin shell is often referred to as mirror buckling.
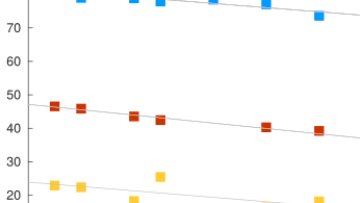
Cycling science is a lucrative and competitive industry in which small advantages are often the difference between winning and losing. For example, the 2017 Tour de France was won by a margin of less than one minute for a total race time of more than 86 hours. Such incremental improvements in performance come from a wide range of specialists, including sports scientists, engineers, and dieticians. How can mathematics assist us?
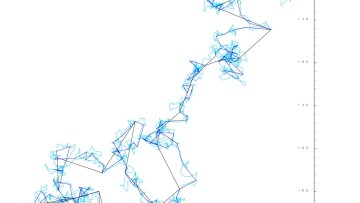
Oxford Mathematician Ilya Chevyrev talks about his research into using stochastic analysis to understand complex systems.
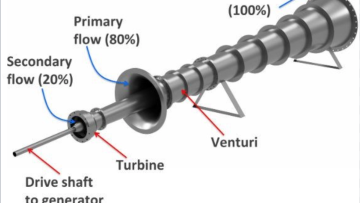
The generation of electricity from elevated water sources has been the subject of much scientific research over the last century. Typically, in order to produce cost-effective energy, hydropower stations require large flow rates of water across large pressure drops. Although there are many low head sites around the UK, including numerous river weirs and potential tidal sites, the pursuit of low head hydropower is often avoided because it is uneconomic.
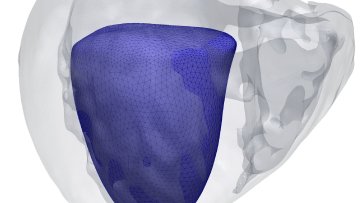
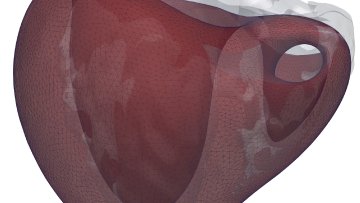
Oxford Mathematician Ricardo Ruiz Baier, in collaboration mainly with the biomedical engineer Alessio Gizzi from Campus Bio-Medico, Rome, have come up with a new class of models that couple diffusion and mechanical stress and which are specifically tailored to the study of cardiac electromechanics.
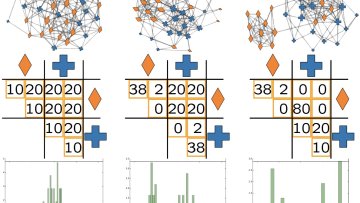
In this collaboration with researchers from the University of Louvain, Renaud Lambiotte from Oxford Mathematics explores the mixing of node attributes in large-scale networks.
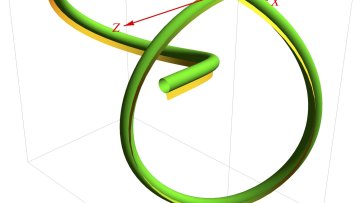
Knots are widespread, universal physical structures, from shoelaces to Celtic decoration to the many variants familiar to sailors. They are often simple to construct and aesthetically appealing, yet remain topologically and mechanically quite complex.
Knots are also common in biopolymers such as DNA and proteins, with significant and often detrimental effects, and biological mechanisms also exist for 'unknotting'.
Oxford Mathematician Andras Juhasz discusses and illustrates his latest research into knot theory.
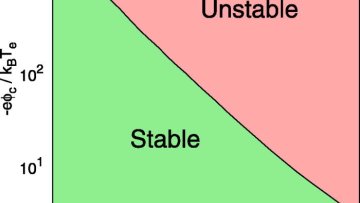
Oxford Mathematician John Allen, Professor Emeritus of Engineering Science, talks about his work on the electrohydrodynamic stability of a plasma-liquid interface. His collaborators are Joshua Holgate and Michael Coppins at Imperial College.
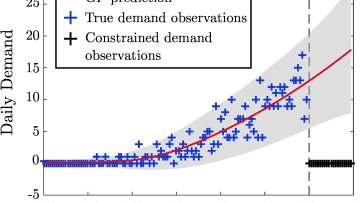
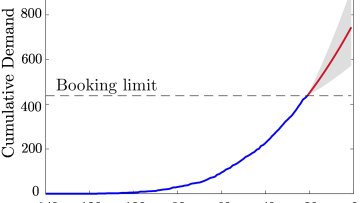
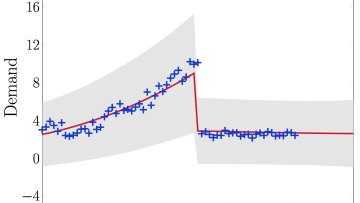
Oxford Mathematicians Ilan Price and Jaroslav Fowkes discuss their work on unconstraining demand with Gaussian Processes.
"One of the key revenue management challenges which airlines, hotels, cruise ships (and other industries) all share is the need to make business decisions in the face of constrained (or censored) demand data.
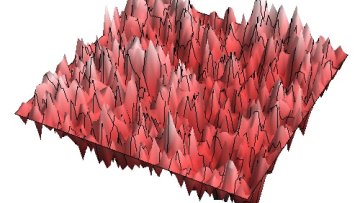
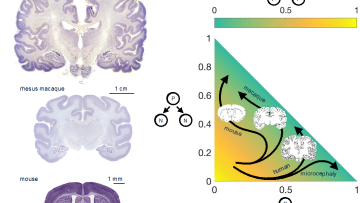
The brain is the most complicated organ of any animal, formed and sculpted over 500 million years of evolution. And the cerebral cortex is a critical component. This folded grey matter forms the outside of the brain, and is the seat of higher cognitive functions such as language, episodic memory and voluntary movement.
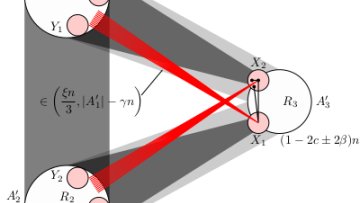
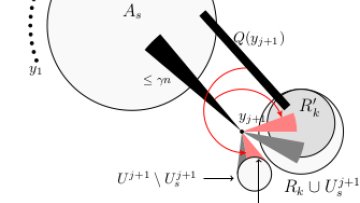
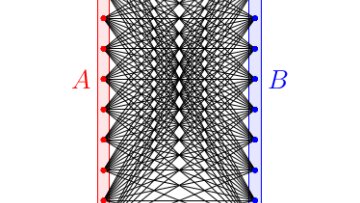
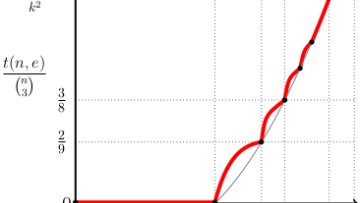
Oxford Mathematician Katherine Staden provides a fascinating snapshot of the field of combinatorics, and in particular extremal combinatorics, and the progress that she and her collaborators are making in answering one of its central questions posed by Paul Erdős over sixty years ago.