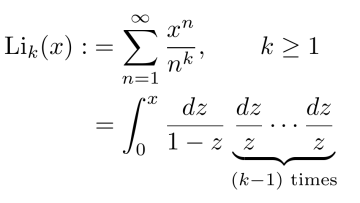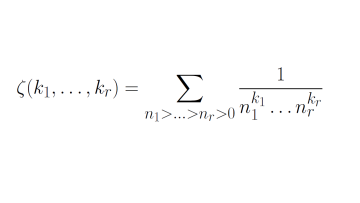Oxford Mathematician Ma Luo talks about his work on constructing iterated integrals, which generalizes usual integrals, to study elliptic and modular curves.
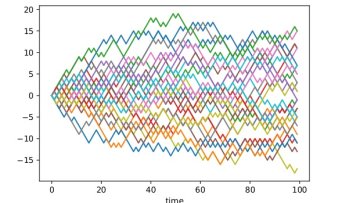
Oxford Mathematicians Andy Allan and Sam Cohen talk about their recent work on estimating with uncertainty.
Oxford Mathematician Nils Matthes talks about trying to understand old numbers using new techniques.
"The Riemann zeta function is arguably one of the most important objects in arithmetic. It encodes deep information about the whole numbers; for example the celebrated Riemann hypothesis, which gives a precise location of its zeros, predicts deep information about the prime numbers. In my research, I am mostly interested in the special values of the Riemann zeta function at integers $k\geq 2$,
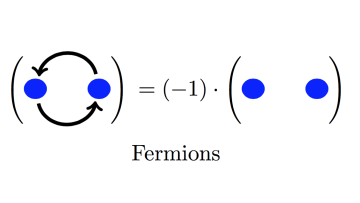
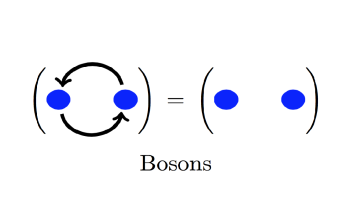
Elementary particles in two dimensional systems are not constrained by the fermion-boson alternative. They are so-called "anyons''. Anyon systems are modelled by modular tensor categories, and form an active area of research. Oxford Mathematician André Henriques explains his interest in the question.
Minimal Lagrangians are key objects in geometry, with many connections ranging from classical problems through to modern theoretical physics, but where and how do we find them? Oxford Mathematician Jason Lotay describes some of his research on these questions.
"A classical problem in geometry going back at least to Ancient Greece is the so-called isoperimetric problem: what is the shortest curve in the plane enclosing a given area A? The answer is a circle:
The 1918 Spanish influenza pandemic claimed around fifty million lives worldwide. Interventions were introduced to reduce the spread of the virus, but these were not based on quantitative assessments of the likely effects of different control strategies. One hundred years later, mathematical modelling is routinely used for forecasting and to help plan interventions during outbreaks in populations of humans, animals and plants.
Have you ever picked up a glass to find that the coaster it was resting on remains stuck to the bottom? If so, then you have experienced the ability of fluid to stick two surfaces together. When the bottom of the glass is wetted, for example by accidentally spilling a drink, then this fluid can fill the gap between the glass and coaster. The surface tension of the liquid then provides a pulling force on the coaster that keeps it attached to the glass.
From nanophotonics to aeroplanes, there are many applications that involve scattering in unbounded domains. Typically, one is interested in situations and geometries where there are no known analytical solutions and one has to resort to numerical algorithms to solve the problem using a computer. Such numerical algorithms should give physically meaningful solutions and hopefully obtain them with the minimal computational cost and time.
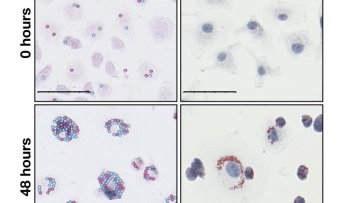
Certain inflammatory and infectious diseases, including atherosclerosis and tuberculosis, are caused by the accumulation inside immune cells of harmful substances, such as lipids and bacteria. A multidisciplinary study published in Proceedings B of the Royal Society, by researchers from the Universities of Oxford and Sydney, has shown how cell cannibalism contributes to this process.
Snap-through buckling is a type of instability in which an elastic object rapidly jumps from one state to another. Such instabilities are familiar from everyday life: you have probably been soaked by an umbrella flipping upwards in high winds, while snap-through is harnessed to generate fast motions in applications ranging from soft robotics to artificial heart valves.
Oxford Mathematician Ian Griffiths talks about his work with colleagues Galina Printsypar and Maria Bruna on modelling the most efficient filters for uses as diverse as blood purification and domestic vacuum cleaners.
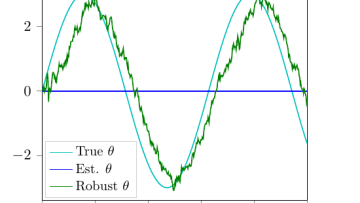
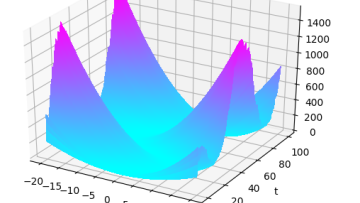
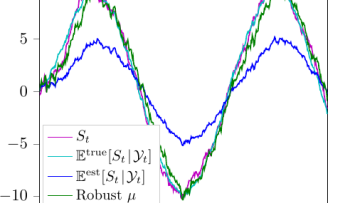
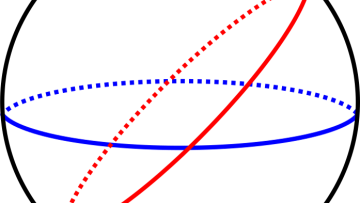
Oxford Mathematician Harald Oberhauser talks about some of his recent research that combines insights from stochastic analysis with machine learning:
The formation of liquid drop patterns on solid surfaces is a fundamental process for both industry and nature. Now, a team of scientists including Oxford Mathematician Andreas Münch and colleagues from the Weierstrass Institute in Berlin, and the University of Saarbrücken can explain exactly how it happens.
Oxford Mathematician Joni Teräväinen talks about his work concerning prime factorisations of consecutive integers and its applications in number theory.
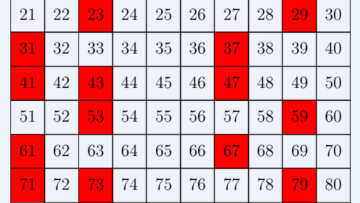
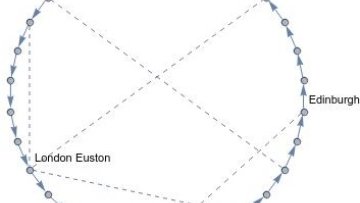
Oxford Mathematician Ebrahim Patel talks about his work using max-plus algebra to improve airport scheduling and to define optimal railway networks.
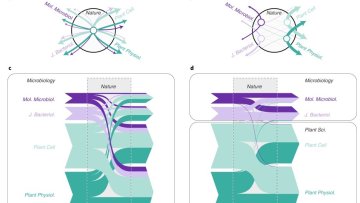
In this collaboration with researchers from the Umeå University and the University of Zurich, Renaud Lambiotte from Oxford Mathematics explores the use of higher-order networks to analyse complex data.
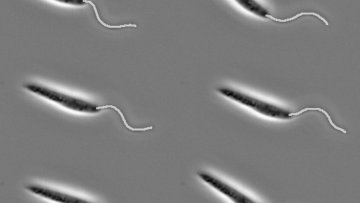
Oxford Mathematician Benjamin Walker talks about his work on the automatic identification of flagella from images, opening up a world of data-driven analysis.
Oxford Mathematician Vinayak Abrol talks about his and colleagues's work on using mathematical tools to provide insights in to deep learning.
Why it Matters!