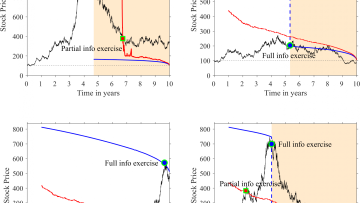
Executive stock options (ESOs) are contracts awarded to employees of companies, which confer the right to reap the profit from buying the company stock (exercising the ESO) at or before a fixed maturity time $T$, for a fixed price specified in the contract (the strike price of the ESO). ESOs are used to augment the remuneration package of employees, the idea being to give them an incentive to boost the company's fortunes, and thus the stock price, making their ESO more valuable.
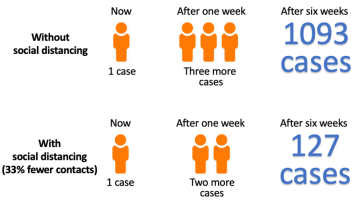
Social distancing measures to reduce the spread of the novel coronavirus are in place worldwide. These guideline are for everyone. We are all expected to reduce our contact with others, and this will have some negative impacts in terms of mental health and loneliness, particularly for the elderly and other vulnerable groups. So why should we follow measures that seem so extreme? The answer is simple. Social distancing works. It reduces transmission of the virus effectively and lessens the impact on already stretched healthcare services.
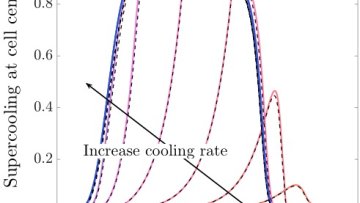
Oxford Mathematician Mohit Dalwadi talks about his work on the modelling of cryopreservation.
Several well-known formulas involving reflection groups of finite-dimensional algebraic systems break down in infinite dimensions, but there is often a predictable way to correct them. Oxford Mathematician Thomas Oliver talks about his research getting to grips with what structures underlie the mysterious correction process.
Oxford Mathematician Andre Guerra talks about quasiconvexity and its role in the Calculus of Variations:
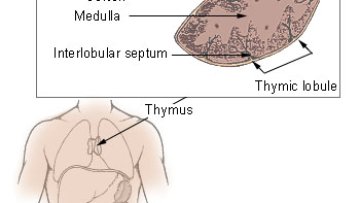
Oxford Mathematician Sam Palmer tackles a crucial issue in our understanding of the risks of serious diseases such as cancer.
Oxford Mathematician Francis Bischoff talks about his recent work on generalized Kähler geometry and the problem of describing its underlying degrees of freedom.
Oxford Mathematician Weijun Xu talks about his exploration of the universal behaviour of large random systems:
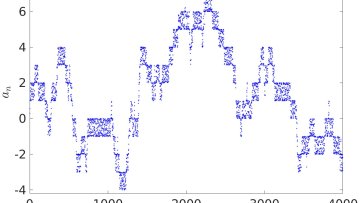
"Nature comes with a separation of scales. Systems that have apparently different individual interactions often behave very similarly when looked at from far away. This phenomenon is particularly attractive when randomness is involved.
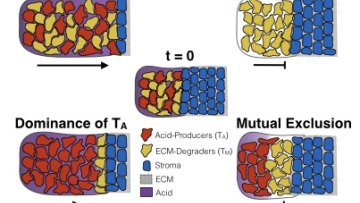
Mathematics has long played a crucial role in understanding ecological dynamics in a range of ecosystems, from classical models of predators and prey to more recent models of aquatic organisms' interaction with global climate. When we think of ecosystems we usually imagine coral reefs or tropical forests; however, over the past decade a substantial effort has emerged in studying a tiny, yet deadly ecosystem: human tumours. Rather than being a single malignant mass, tumours are living and evolving ecosystems.
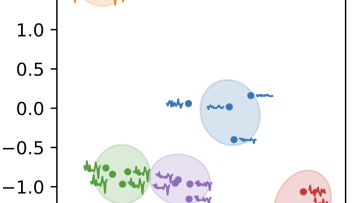
Networks provide powerful tools and methods to understand inter-connected systems. What is the most central element in a system? How does its structure affect a linear or non-linear dynamical system, for instance synchronisation? Is it possible to find groups of elements that play the same role or are densely connected with each other? These are the types of questions that can be answered within the realm of network science. For standard algorithms to be used, however, it is usually expected that the underlying network structure is known.
In 2018, the World Health Organization added “Disease X” to its list of priority diseases, alongside diseases like Ebola virus disease and SARS. Disease X is representative of infectious agents that are not currently known to cause cases in humans. In other words, it denotes the possibility of an epidemic of a disease that we have never seen before.
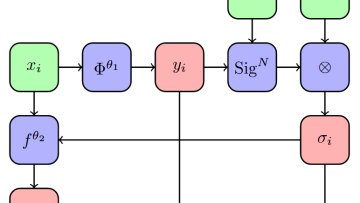
Oxford Mathematician Patrick Kidger talks about his recent work on applying the tools of controlled differential equations to machine learning.
Sequential Data
The changing air pressure at a particular location may be thought of as a sequence in $\mathbb{R}$; the motion of a pen on paper may be thought of as a sequence in $\mathbb{R}^2$; the changes within financial markets may be thought of as a sequence in $\mathbb{R}^d$, with $d$ potentially very large.
Oxford Mathematician Alan Lauder works on elliptic curves and modular forms, and methods for constructing points on the former using the latter. Read more here.
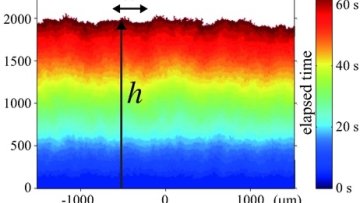
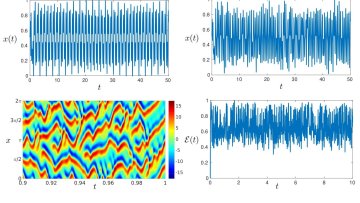
For centuries, engineers have sought to prevent structures from buckling under heavy loads or large impacts, constructing ever larger buildings and safer vehicles. However, recent advances in soft matter are redefining the way we manipulate materials. In particular, an age-old aversion to buckling is being recast in a new light as researchers find that structural instabilities can be harnessed for functionality.
Energy production is arguably one of the most important factors underlying modern civilisation. Energy allows us to inhabit inhospitable parts of the Earth in relative comfort (using heating and air conditioning), create large cities (by efficiently transporting food and pumping water), or maintain our health (providing the energy for water purification). It also connects people by allowing long-distance travel and facilitating digital communication.
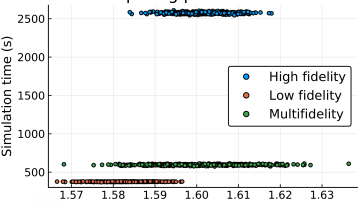
Applied mathematics provides a collection of methods to allow scientists and engineers to make the most of experimental data, in order to answer their scientific questions and make predictions. The key link between experiments, understanding, and predictions is a mathematical model: you can find many examples in our case-studies. Experimental data can be used to calibrate a model by inferring the parameters of a real-world system from its observed behaviour.
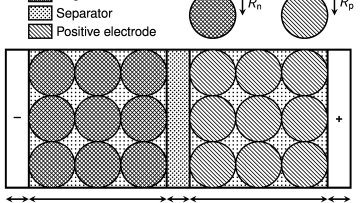
Have you ever wished that the battery on your phone would last longer? That you could charge it up more rapidly? Maybe you have thought about buying an electric vehicle, but were filled with range anxiety – the overwhelming fear that the battery will run out before you reach your destination, leaving you stranded? Oxford Mathematicians are hard at work demonstrating that mathematics may provide the key to help tackle problems faced by the battery industry.