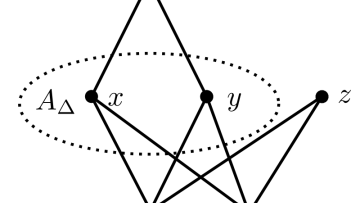
Oxford Mathematician Ric Wade explains how right-angled Artin groups, once neglected, are now central figures in low-dimension topology.
We’re all familiar with liquid droplets moving under gravity (especially if you live somewhere as rainy as Oxford). However, emerging applications such as lab-on-a-chip technologies require precise control of extremely small droplets; on these scales, the forces associated with surface tension become dominant over gravity, and it is therefore not practical to rely on the weight of the drops for motion.
The concept of equilibrium is one of the most central ideas in economics. It is one of the core assumptions in the vast majority of economic models, including models used by policymakers on issues ranging from monetary policy to climate change, trade policy and the minimum wage. But is it a good assumption?
Oxford Mathematician Thomas Prince talks about his work on the construction of Fano manifolds in dimension four and their connection with Calabi-Yau geometry.
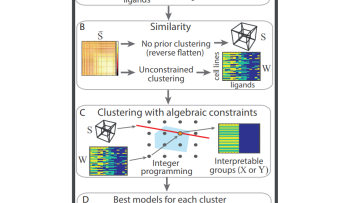
Oxford Mathematicians Anna Seigal, Heather Harrington, Mariano Beguerisse Diaz and colleagues talk about their work on trying to find cancer cell lines with similar responses by clustering them with structural constraints.
Oxford Mathematician Yinan Wang talks about his and colleagues' work on classification of elliptic Calabi-Yau manifolds and geometric solutions of F-theory.
Oxford Mathematician Erik Panzer talks about his and colleagues' work on devising an algorithm to compute Kontsevich's star-product formula explicitly, solving a problem open for more than 20 years.
"The transition from classical mechanics to quantum mechanics is marked by the introduction of non-commutativity. For example, let us consider the case of a particle moving on the real line.
From commutative classical mechanics...
When mathematicians solve a differential equation, they are usually converting unbounded operators (such as differentiation) which are represented in the equation into bounded operators (such as integration) which represent the solutions. It is rarely possible to give a solution explicitly, but general theory can often show whether a solution exists, whether it is unique, and what properties it has. For this, one often needs to apply suitable (bounded) functions $f$ to unbounded operators $A$ and obtain bounded operators $f(A)$ with good properties.&
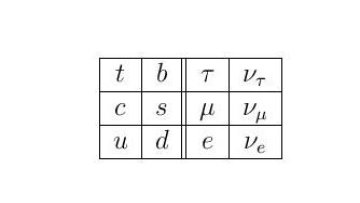
Oxford Mathematician Tsou Sheung Tsun talks about her work on building the Framed Standard Model and the exciting directions it has taken her.
Statistical mechanics (or thermodynamics) is a way of understanding large systems of interacting objects, such as particles in fluids and gases, chemicals in solution, or people meandering through a crowded street. Large macroscopic systems require prohibitively large systems of equations, and so equilibrium thermodynamics gives us a way to average out all of these details and understand the typical behaviour of the large scale system.
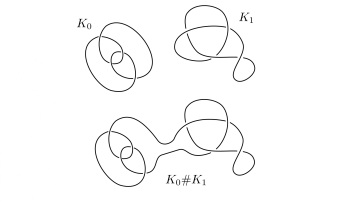
Knots are isotopy classes of smooth embeddings of $S^1$ in to $S^3$. Intuitively a knot can be thought of as an elastic closed curve in space, that can be deformed without tearing. Oxford Mathematician Daniele Celoria explains.
"Knots are ubiquitous in the study of the topological and geometrical properties of manifolds with dimension $3$ and $4$. This is due to the fact that they can be used to prescribe the attachment instructions for the "building blocks" of these spaces, through a process known as surgery.
Homogenization theory aims to understand the properties of materials with complicated microstructures, such as those arising from flaws in a manufacturing process or from randomly deposited impurities. The goal is to identify an effective model that provides an accurate approximation of the original material. Oxford Mathematician Benjamin Fehrman discusses his research.
"The practical considerations for identifying a simplified model are twofold:
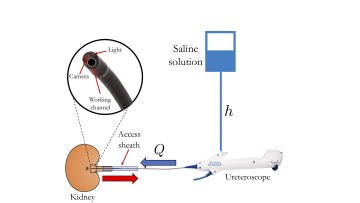
The discomfort experienced when a kidney stone passes through the ureter is often compared to the pain of childbirth. Severe pain can indicate that the stone is too large to naturally dislodge, and surgical intervention may be required. A ureteroscope is inserted into the ureter (passing first through the urethra and the bladder) in a procedure called ureteroscopy. Via a miniscule light and a camera on the scope tip, the patient’s ureter and kidney are viewed by a urologist.
The Sun has been emitting light and illuminating the Earth for more than four billion years. By analyzing the properties of solar light we can infer a wealth of information about what happens on the Sun. A particularly fascinating (and often overlooked) property of light is its polarization state, which characterizes the orientation of the oscillation in a transverse wave. By measuring light polarization, we can gather precious information about the physical conditions of the solar atmosphere and the magnetic fields present therein.
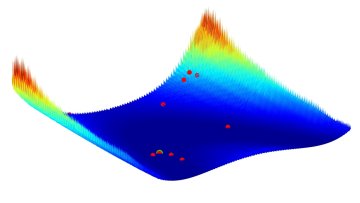
The problem of optimisation – that is, finding the maximum or minimum of an ‘objective’ function – is one of the most important problems in computational mathematics. Optimisation problems are ubiquitous: traders might optimise their portfolio to maximise (expected) revenue, engineers may optimise the design of a product to maximise efficiency, data scientists minimise the prediction error of machine learning models, and scientists may want to estimate parameters using experimental data.
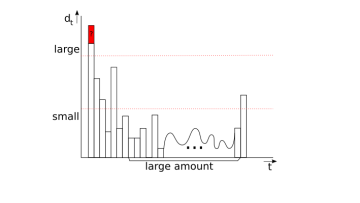
Diophantine approximation is about how well real numbers can be approximated by rationals. Say I give you a real number $\alpha$, and I ask you to approximate it by a rational number $a/q$, where $q$ is not too large. A naive strategy would be to first choose $q$ arbitrarily, and to then choose the nearest integer $a$ to $q \alpha$. This would give $| \alpha - a/q| \le 1/(2q)$, and $\pi \approx 3.14$.