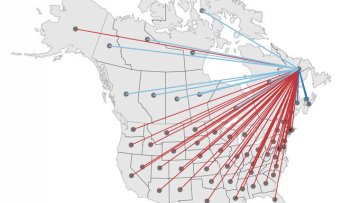
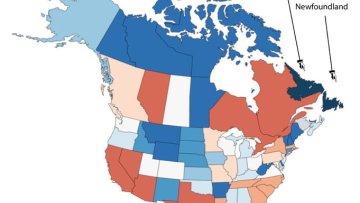
When Oxford Mathematician Alain Goriely was approached by his collaborator Ellen Kuhl from Stanford University to work on a travel restriction issue in Newfoundland he started a Coronavirus journey that ended up in the Canadian Supreme Court.
Oxford Mathematician Daniel Gulotta talks about his work on $p$-adic geometry and the Langlands program.
"Geometry is one of the more visceral areas of mathematics. Concepts like distance and curvature are things that we can actually see and feel.
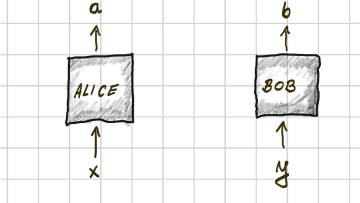
Oxford Mathematician Artur Ekert describes how his research in to using Quantum properties for cryptography led to some very strange results.
Oxford Mathematician Vidit Nanda discusses his recent work with colleagues Bernadette Stolz, Jared Tanner and Heather Harrington on detecting singularities in data.
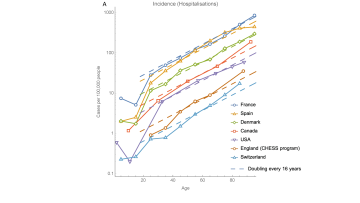
One of the great puzzles of the current COVID-19 crisis is the observation that older people have a much higher risk of becoming seriously ill. While it is usually commonly accepted that the immune system fails progressively with age, the actual mechanism leading to this effect was not fully understood. In a recent work, Sam Palmer from Oxford Mathematics and his colleagues in Cambridge have proposed a simple and elegant solution to this puzzle.
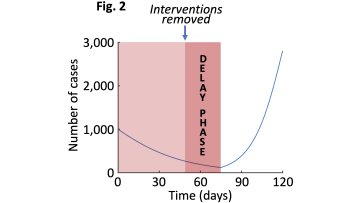
Mathematical models have been used throughout the COVID-19 pandemic to help plan public health measures. Attention is now turning to how interventions can be removed while continuing to restrict transmission. Predicting the effects of different possible COVID-19 exit strategies is an important current challenge requiring mathematical modelling, but many uncertainties remain.
A set of integers greater than 1 is primitive if no number in the set divides another. Erdős proved in 1935 that the series of $1/(n \log n)$ for $n$ running over a primitive set A is universally bounded over all choices of A. In 1988 he conjectured that the universal bound is attained for the set of prime numbers. In this research case study, Oxford's Jared Duker Lichtman describes recent progress towards this problem:
For thirty years Oxford Mathematician Roger Penrose has challenged one of the key planks of Cosmology, namely the concept of Inflation, now over 40 years old, according to which our universe expanded at an enormous rate immediately after the Big Bang. Instead, fifteen years ago, Penrose proposed a counter-concept of Conformal Cyclic Cosmology by which Inflation is moved to before the Big Bang and which introduces the idea of preceding aeons.
Ben Green and collaborators discover that the well-known "birthday paradox" has its equivalent in the divisors of a typical integer.
"The well-known "birthday paradox'' states that if you have 23 or more people in a room - something difficult to achieve nowadays without a very large room - then the chances are better than 50:50 that some pair of them will share a birthday. If we could have a party of 70 or more people, the chance of this happening rises to 99.9 percent.
Oxford Mathematician Christopher Hollings and Oxford Egyptologist Richard Bruce Parkinson explain how our interpretation of Egyptian Mathematics has changed over the past two centuries and what that says about how historians of mathematics approach their subject.
In modern Cryptography, the security of every cryptosystem is required to be formally proven. Most of the time, such formal proof is by contradiction: it shows that there cannot exist an adversary that breaks a specific cryptosystem, because otherwise the adversary would be able to solve a hard mathematical problem, i.e. a problem that needs an unfeasible amount of time (dozens of years) to be concretely solved, even with huge computational resources.
How do we design face masks that efficiently remove contaminants while ensuring that we can still breathe easily? One complicating factor with this question is the fact that the properties of the material that we start off with for our face mask can be very different when in use. A key example is seen when you stretch the mask around your face to put it on. In doing so, you also stretch the pores, i.e., the holes in the material that allow the air to pass through.
Oxford Mathematician Katherine Staden talks about the mathematics of seating plans.
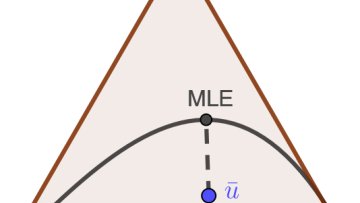
Oxford Mathematician Anna Seigal talks about her work on connecting invariant theory with maximum likelihood estimation.
Oxford Mathematician Ben Green on how and why he has been pondering footballs in high dimensions.
"A 3-dimensional football is usually a truncated icosahedron. This solid has the virtue of being pleasingly round, hence its widespread use as a football. It is also symmetric in the sense that there is no way to tell two different vertices apart: more mathematically, there is a group of isometries of $\mathbf{R}^3$ acting transitively on the vertices.
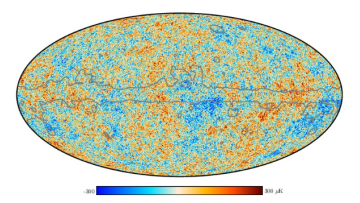
Oxford Mathematicians Dmitry Belyaev and Michael McAuley explain the ubiquitous role of Gaussian Fields in modelling spatial phenomena across science, and especially in cosmology. This case-study is based on work with Stephen Muirhead at Queen Mary University of London (QMUL).
The International Congress of Mathematicians (ICM) that was held in Oslo in July 1936 was a unique event that took place in turbulent times, research by Oxford Mathematician Christopher Hollings has revealed.
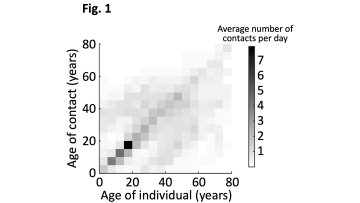
The Coronavirus disease pandemic (COVID-19) poses unprecedented challenges for governments and societies around the world. In addition to medical measures, non-pharmaceutical measures have proven to be critical for delaying and containing the spread of the virus. However, effective and rapid decision-making during all stages of the pandemic requires reliable and timely data not only about infections, but also about human behaviour, especially on mobility and physical co-presence of people.