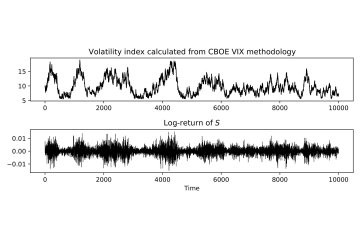
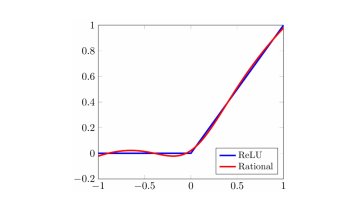
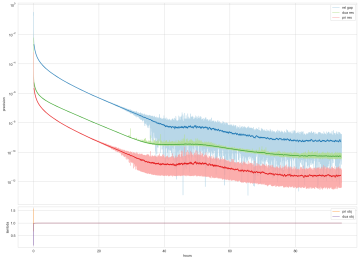
Oxford Mathematicians Samuel N. Cohen, Christoph Reisinger and Sheng Wang have developed new methods to help machine learning build economically reasonable models for options markets. By embedding no-arbitrage restrictions within a neural network, more trustworthy and realistic models can be built, allowing for better risk management in the banking system.
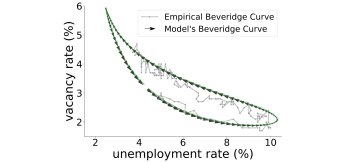
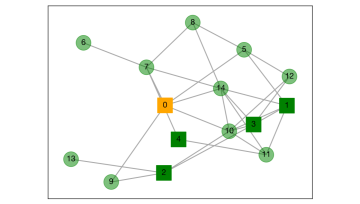
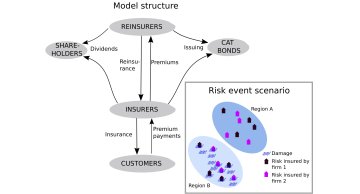
Oxford Mathematicians and Economists Maria del Rio-Chanona, Penny Mealy, Mariano Beguerisse-Díaz, François Lafond, and J. Doyne Farmer discuss their network model of labor market dynamics.
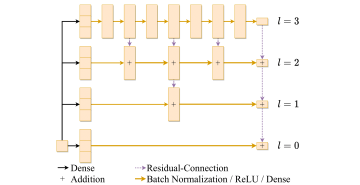
Deep learning has become an important topic across many domains of science due to its recent success in image recognition, speech recognition, and drug discovery. Deep learning techniques are based on neural networks, which contain a certain number of layers to perform several mathematical transformations on the input.
Oxford Mathematician Arkady Wey discusses a stochastic agent-based model of the workplace, developed to explore the importance of compliance with test and trace programs following a pandemic lockdown.
Oxford Mathematician Ben Green on a tale of conjectures, mistaken assumptions and eventual solutions: a tale of mathematics.
"The famous discrete mathematician Ron Graham sadly passed away last year. I did not know him well, but I had the pleasure of meeting him a few times. On the first such occasion, in Vancouver in 2004, he mentioned one of his favourite open questions over lunch. This concerns the size of certain "van der Waerden numbers", a kind of arithmetic variant of graph Ramsey numbers.
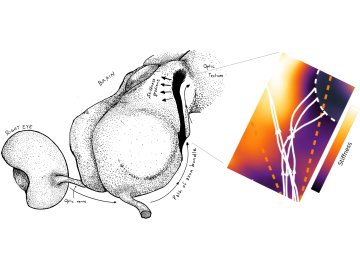
During the early growth of the brain, an extraordinary process takes place where axons, neurons, and nerves extend, grow, and connect to form an intricate network that will be used for all brain activities and cognitive processes. A fundamental scientific question is to understand the laws that these growing cells follow to find their correct target.
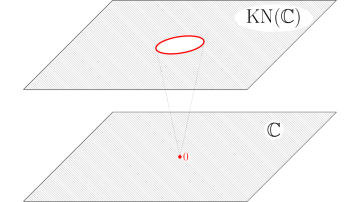
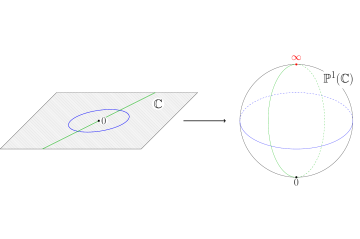
Oxford Mathematcian Clemens Koppensteiner talks about his work on the geometry and topology of compactifications.
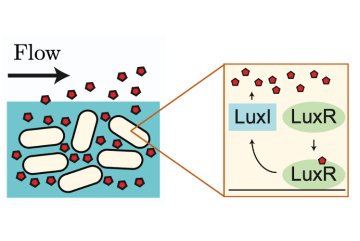
By pooling resources between cells, colonies of bacteria can exhibit behaviours far beyond the capabilities of an individual bacterium. For example, bacterial populations can encase themselves in a self-generated polymer matrix that shelters cells in the core of the population from the external environment. Such communities are termed “bacterial biofilms”, and show increased tolerance to antimicrobial treatments such as antibiotics.
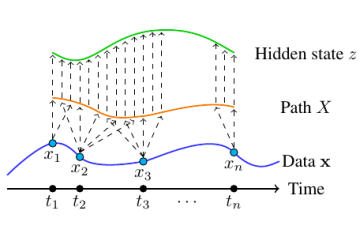
Oxford Mathematician Patrick Kidger writes about combining the mathematics of differential equations with the machine learning of neural networks to produce cutting-edge models for time series.
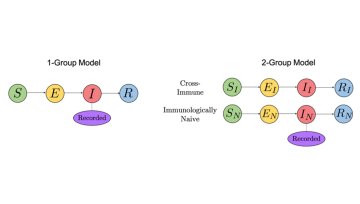
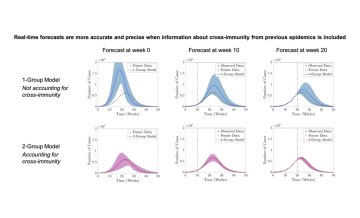
How to deal with resistance? This is the headline question these days with regards to COVID vaccines. But it is an important question also in cancer therapy. Over the past century, oncology has come a long way, but all too often cancers still recur due to the emergence of drug-resistant tumour cells. How to tackle these cells is one of the key questions in cancer research. The main strategy so far has been the development of new drugs to which the resistant cells are still sensitive.
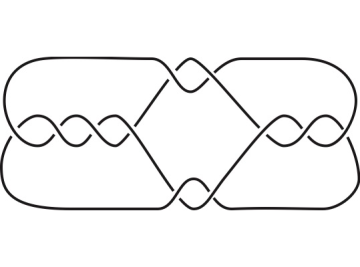
Take a piece of rope and knot it as you wish. When you are done, glue the two extremities together and you will obtain a physical realisation of what mathematicians also call a knot: a simple closed curve in 3-dimensional space. Now, put the knotted rope on a table and take a picture of it from above. It is now a planar projection of your knot. The mathematical equivalent of it is a knot diagram with multiple crossings as shown in the figure.
Oxford Mathematician Vladimir Markovic talks about his research into intrinsic geometry of Teichmüller Spaces.
Social distancing is integral to our lives these days, but distancing also underpins the ordered patterns and arrangements we see all around us in Nature. Oxford Mathematician Priya Subramanian studies the defects in such patterns and shows how they relate to the underlying pattern, i.e. to the distancing itself.
Oxford Mathematician Markus Dablander talks about his collaboration with Julius Berner and Philipp Grohs from the University of Vienna. Together they developed a new deep-learning-based method for the computationally efficient solution of high-dimensional parametric Kolmogorov PDEs.
Oxford Mathematician Daniel Woodhouse talks about the theorem that motivates much of his research.
Oxford Mathematician Dawid Kielak talks about his joint work with Marek Kaluba and Piotr Nowak in which they used a computer* to prove a theorem about the behaviour of other computers.