Towards the end of the eighteenth century, French mathematician and engineer Gaspard Monge considered a problem. If you have a lot of rubble, you would like to have a fort, and you do not like carrying rocks very far, how do you best rearrange your disorganised materials into organised walls? Over the two centuries since then, his work has been developed into the rich mathematical theory of optimal transport.
In quantum many body physics, we look for universal features that allow us to classify complex quantum systems. This classification leads to phase diagrams of quantum systems. These are analogous to the familiar phase diagram of water at different temperatures and pressures, with ice and vapour constituting two phases. Quantum phase diagrams correspond to the different phases of matter at zero temperature, where the system is in its lowest energy state (usually called the ground state).
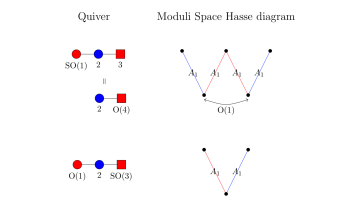
One of the main themes of geometry in recent years has been the appearance of unexpected dualities between different geometric spaces arising from ideas in mathematical physics. One famous such example is mirror symmetry. Another kind of duality, which I am currently investigating with collaborators from Oxford and Imperial College, is symplectic duality.
Knot theory studies embeddings of the circle into the three dimensional space and the first knot invariant was the Alexander polynomial. The world of quantum invariants started with the milestone discovery of the Jones polynomial and was expanded by Reshetikhin and Turaev’s algebraic construction which starts from a quantum group and leads to link invariants.
Oxford Mathematician Lukas Brantner explains how generalised Lie algebras lead to new insights in Galois theory, deformation theory, and the theory of configuration spaces. Lukas has just been awarded a Royal Society University Research Fellowship.
Oxford Mathematician Aymeric Vie, first year DPhil student at the Centre for Doctoral Training, Mathematics of Random Systems, describes his work on the population network structure of genetic algorithms.This work identifies new ways to improve the performance of those stochastic algorithms, and has received a Best Paper Award at the Genetic and Evolutionary Computation Conference 2021.
Oxford Mathematician Connor Behan discusses the ways in which a free quantum field can be coupled to a spatial boundary. His recent work with Lorenzo di Pietro, Edoardo Lauria and Balt van Rees sheds light on this question using the non-perturbative bootstrap technique.
What takes a mathematician to the Arctic? In short, context. The ice of the Arctic Ocean has been a rich source of mathematical problems since the late 19th century, when Josef Stefan, aided by data from expeditions that went in search of the Northwest Passage, developed the classical Stefan problem. This describes the evolution of a moving boundary at which a material undergoes a phase change. In recent years, interest in the Arctic has only increased, due to the rapid changes occurring there due to climate change.
Oxford Mathematician William Hart and former Oxford Mathematician Dr Robin Thompson (now an Assistant Professor at the University of Warwick) discuss their latest joint COVID-19 research (carried out with fellow Oxford Mathematician Philip Maini), using mathematical models to infer changes in infectiousness during SARS-CoV-2 infections.
Oxford Mathematicians Samuel N. Cohen, Christoph Reisinger and Sheng Wang have developed new methods to help machine learning build economically reasonable models for options markets. By embedding no-arbitrage restrictions within a neural network, more trustworthy and realistic models can be built, allowing for better risk management in the banking system.
Oxford Mathematicians and Economists Maria del Rio-Chanona, Penny Mealy, Mariano Beguerisse-Díaz, François Lafond, and J. Doyne Farmer discuss their network model of labor market dynamics.
Deep learning has become an important topic across many domains of science due to its recent success in image recognition, speech recognition, and drug discovery. Deep learning techniques are based on neural networks, which contain a certain number of layers to perform several mathematical transformations on the input.
Oxford Mathematician Arkady Wey discusses a stochastic agent-based model of the workplace, developed to explore the importance of compliance with test and trace programs following a pandemic lockdown.
Oxford Mathematician Ben Green on a tale of conjectures, mistaken assumptions and eventual solutions: a tale of mathematics.
"The famous discrete mathematician Ron Graham sadly passed away last year. I did not know him well, but I had the pleasure of meeting him a few times. On the first such occasion, in Vancouver in 2004, he mentioned one of his favourite open questions over lunch. This concerns the size of certain "van der Waerden numbers", a kind of arithmetic variant of graph Ramsey numbers.
During the early growth of the brain, an extraordinary process takes place where axons, neurons, and nerves extend, grow, and connect to form an intricate network that will be used for all brain activities and cognitive processes. A fundamental scientific question is to understand the laws that these growing cells follow to find their correct target.
In the 1680s there was a coffee house in London by the name of "Lloyd's". This place, catering to early maritime insurers, lent its name to the nascent English insurance market place, the now famous Lloyd's of London.
Oxford Mathematcian Clemens Koppensteiner talks about his work on the geometry and topology of compactifications.
By pooling resources between cells, colonies of bacteria can exhibit behaviours far beyond the capabilities of an individual bacterium. For example, bacterial populations can encase themselves in a self-generated polymer matrix that shelters cells in the core of the population from the external environment. Such communities are termed “bacterial biofilms”, and show increased tolerance to antimicrobial treatments such as antibiotics.